题目内容
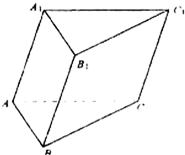如图，用四种不同颜色给三棱柱ABC-A1B1C1的六个顶点涂色，要求四种颜色全都用上，每个点涂一种颜色，且图中每条线段的两个端点涂不同颜色．则不同的涂色方法的种数为考点：计数原理的应用
专题：排列组合
分析：根据题意，分3步进行，第一步，为A、B、C三点涂色，由排列数公式可得其情况数目，第二步，在A1、B1、C1中选一个涂第4种颜色，第三步，为剩下的两个点涂色，分类讨论可得其情况数目，进而由分步计数原理，计算可得答案．
解答：
解：根据题意，四种颜色全都用上，每个点涂一种颜色，
第一步，为A、B、C三点涂色共有A43种；
第二步，在A1、B1、C1中选一个涂第4种颜色，有3种情况；
第三步，为剩下的两点涂色，
假设剩下的为B1、C1，若B1与A同色，则C1只能选B点颜色；若B1与C同色，
则C1有A、B处两种颜色涂．
故为B1、C1共有3种涂法，
即剩下的两个点有3种情况，
则共有A43×3×3=216种方法．
故答案为：216．
第一步，为A、B、C三点涂色共有A43种；
第二步，在A1、B1、C1中选一个涂第4种颜色，有3种情况；
第三步，为剩下的两点涂色，
假设剩下的为B1、C1，若B1与A同色，则C1只能选B点颜色；若B1与C同色，
则C1有A、B处两种颜色涂．
故为B1、C1共有3种涂法，
即剩下的两个点有3种情况，
则共有A43×3×3=216种方法．
故答案为：216．
点评：本题考查了分类计数原理与分步计数原理的运用，排列、组合在计数中的应用，合理分类，恰当分步是解决本题的关键．
练习册系列答案
相关题目