题目内容

已知向量
a
=（1，x），
b
=（x2，2），则（2
a
）•
b
的最小值为
 
．
考点：平面向量数量积的运算
专题：平面向量及应用
分析：利用向量的数量积的坐标运算将（2
a
）•
b
用x表示．
解答： 解：∵向量
a
=（1，x），
b
=（x2，2），
∴（2
a
）•
b
=2x2+4x=2（x+1）2-2，
∴（2
a
）•
b
的最小值为的-2．
故答案为：-2．
点评：本题考查了向量的数量积的坐标运算以及二次函数最值的求法．
练习册系列答案
相关题目
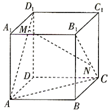如图，棱长为2的正方体ABCD-A1B1C1D1中，M，N分别是线段AD1和B1C上的动点，且满足D1M=CN，则下列命题正确的是
 
．（把所有正确命题的序号都填上）
①存在M，N的某一位置，使AB∥MN；
②△BMN的面积为定值；
③当D1M＞0时，直线MB1与AN是异面直线；
④无论M，N运动到任一位置，均有BC⊥MN；
⑤M，N在运动过程中，线段MN在平面ADA1D1内的射影所形成区域的面积为2．
若对任意x＞0，a≥
3
x
x2-3x+3
恒成立，则a的取值范围是
 
．
已知直线l过抛物线y=2x2的焦点，交抛物线于A，B两点，则|AB|的最小值为
 
．
直线4x-3y+2=0与直线8x-6y-1=0的距离为
 
．
若sin（180°+α）=
1
10
，则
1
cos(-α)
+sin(-α-900)
1
sin(5400-α)
-cos(-α-2700)
=
 
．
比较大小 log20.5
 
log0.20.1．
在长方体ABCD-A1B1C1D1中，AB=2，AD=2，CC1=，则二面角C1-BD-C的大小为
 
．
若函数f（x）=a|x-b|+2在[0，+∞）上为增函数，则实数a，b的取值范围是（　　）
A、a＞0，b＜0
B、a＞0，b≤0
C、a＜0，b≤0
D、a=1，b≥0

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网