题目内容
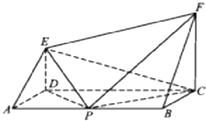 如图,ABCD为矩形,CF⊥平面ABCD,DE⊥平面ABCD,AB=4a,BC=CF=2a,p为AB的中点.
如图,ABCD为矩形,CF⊥平面ABCD,DE⊥平面ABCD,AB=4a,BC=CF=2a,p为AB的中点.(Ⅰ)求证:面FBC∥面EAD;
(Ⅱ)求证:平面PCF⊥平面PDE;
(Ⅲ)求四面体PCEF的体积.
考点:棱柱、棱锥、棱台的体积,平面与平面平行的判定,平面与平面垂直的判定
专题:空间位置关系与距离
分析:(Ⅰ)由已知得AD∥BC,DE∥CF,由此能证明面FBC∥面EAD.
(Ⅱ)由已知得PD⊥PC,PD⊥CF,由此能证明平面PCF⊥平面PDE,
(Ⅲ)由PD⊥平面PFC,PC=PD=2
a,CF⊥平面ABCD,CF=2a,能求出四面体PCEF的体积.
(Ⅱ)由已知得PD⊥PC,PD⊥CF,由此能证明平面PCF⊥平面PDE,
(Ⅲ)由PD⊥平面PFC,PC=PD=2
| 2 |
解答:
(Ⅰ)证明:∵ABCD为矩形,∴AD∥BC,
∵CF⊥平面ABCD,DE⊥平面ABCD,
∴DE∥CF,
∵BC,CF?平面BCF,且BC∩CF=C,
∴面FBC∥面EAD.
(Ⅱ)证明:在矩形ABCD中,由AP=BP=2a,得PC=PD=2
a,
又CD=4a,由勾股定理,得PD⊥PC,
∵CF⊥平面ABCD,则PD⊥CF,
由PC∩CF=C,得PD⊥平面PFC,
∴PD?平面PDE,
∴平面PCF⊥平面PDE,
(Ⅲ)解:∵PD⊥平面PFC,PC=PD=2
a,
CF⊥平面ABCD,CF=2a,
∴S△PFC=
×PC×FC=
×2
a×2a=2
a2,
∴四面体PCEF的体积:
V=
S△PFC×PD=
×2
a2×2
a=
.
∵CF⊥平面ABCD,DE⊥平面ABCD,
∴DE∥CF,
∵BC,CF?平面BCF,且BC∩CF=C,
∴面FBC∥面EAD.
(Ⅱ)证明:在矩形ABCD中,由AP=BP=2a,得PC=PD=2
| 2 |
又CD=4a,由勾股定理,得PD⊥PC,
∵CF⊥平面ABCD,则PD⊥CF,
由PC∩CF=C,得PD⊥平面PFC,
∴PD?平面PDE,
∴平面PCF⊥平面PDE,
(Ⅲ)解:∵PD⊥平面PFC,PC=PD=2
| 2 |
CF⊥平面ABCD,CF=2a,
∴S△PFC=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
∴四面体PCEF的体积:
V=
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 2 |
| 8a3 |
| 3 |
点评:本题考查空间线面关系、几何体的体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
已知
=(1-t,1-t,t),
=(2,t,t),则|
-
|的最小值是( )
| a |
| b |
| b |
| a |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
双曲线y2-3x2=9的渐近线方程为( )
A、x±
| ||
| B、x±3y=0 | ||
C、
| ||
| D、3x±y=0 |
某几何体的三视图如图所示,则该几何体的体积为( )


| A、16+8π |
| B、8+8π |
| C、16+16π |
| D、8+16π |
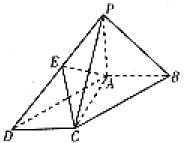 如图,四棱锥P-ABCD的底面是平行四边形,PA⊥平面ABCD,AC⊥AB,点E是PD的中点.
如图,四棱锥P-ABCD的底面是平行四边形,PA⊥平面ABCD,AC⊥AB,点E是PD的中点.
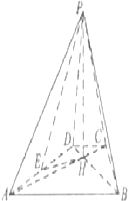 如图,已知四棱锥P-ABCD的底面为等腰梯形,AB∥CD,AC⊥BD垂足为H,PH是四棱锥的高,E为AD的中点.
如图,已知四棱锥P-ABCD的底面为等腰梯形,AB∥CD,AC⊥BD垂足为H,PH是四棱锥的高,E为AD的中点.