题目内容
已知P是以F1F2为焦点的双曲线
-
=1(a>0,b>0)上一点,若
•
=0,且∠PF1F2=30°,|F1F2|=2,则该双曲线的离心率为 .
| x2 |
| a2 |
| y2 |
| b2 |
| PF1 |
| PF2 |
考点:双曲线的简单性质
专题:计算题,平面向量及应用,圆锥曲线的定义、性质与方程
分析:由条件可得P在右支上,PF2=c,PF1=
c,再由双曲线的定义,可得a,c的关系,再由离心率公式计算即可得到.
| 3 |
解答:
解:因为
•
=0,
则PF1⊥PF2且∠PF1F2=30°,P在右支上,
所以PF2=c,PF1=
c,
又PF1-PF1=2a=
c-c,
所以e=
=
=
+1,
即双曲线的离心率为
+1,
故答案为:
+1.
| PF1 |
| PF2 |
则PF1⊥PF2且∠PF1F2=30°,P在右支上,
所以PF2=c,PF1=
| 3 |
又PF1-PF1=2a=
| 3 |
所以e=
| c |
| a |
| 2 | ||
|
| 3 |
即双曲线的离心率为
| 3 |
故答案为:
| 3 |
点评:本题考查双曲线的离心率,考查双曲线的定义,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
已知抛物线C:y2=4x,点P(m,0),O为坐标原点,若在抛物线C上存在一点Q,使得∠OQP=90°,则实数m的取值范围是( )
| A、(4,8) |
| B、(4,+∞) |
| C、(0,4) |
| D、(8,+∞) |
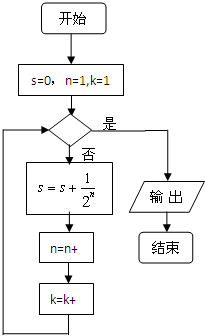
如图是计算
+
+
+
+
值的一个程序框图,其中判断框内应填入的条件是( )
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 16 |
| 1 |
| 32 |

| A、K>5? | B、K<5? |
| C、K>10? | D、K<10? |
阅读程序框图,若输入m=1,n=2,则输出n=( )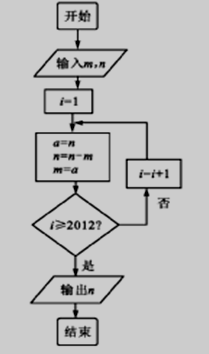

| A、1 | B、-1 | C、2 | D、-2 |
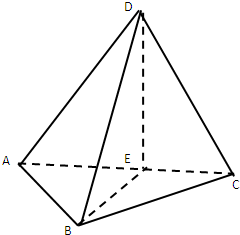 如图,三棱锥D-ABC中,AB=BC=2,BD=3,∠ABC=∠DBA=∠DBC=60°,E为AC的中点.
如图,三棱锥D-ABC中,AB=BC=2,BD=3,∠ABC=∠DBA=∠DBC=60°,E为AC的中点.