题目内容
双曲线
-
=1的离心率e=( )
| x2 |
| 4 |
| y2 |
| 5 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:求出双曲线的a,b,c,再由离心率公式e=
,计算即可得到.
| c |
| a |
解答:
解:双曲线
-
=1的a=2,b=
,
则c=
=3,
则e=
=
.
故选A.
| x2 |
| 4 |
| y2 |
| 5 |
| 5 |
则c=
| a2+b2 |
则e=
| c |
| a |
| 3 |
| 2 |
故选A.
点评:本题考查双曲线的方程和性质,考查离心率的求法,考查运算能力,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知m,n为两条不同的直线,α,β为两个不同的平面,且n?β,则下列叙述正确的是( )
| A、m∥n,m?α⇒α∥β |
| B、m∥n,m⊥α⇒α⊥β |
| C、α⊥β,m⊥n⇒n∥α |
| D、α∥β,m?α⇒m∥n |
设x2+y2+z2=1,若λxyz≤
对一切x,y,z∈R*均成立,则λ的最大值为( )
| 1+z |
| 2 |
A、2(
| ||||
B、
| ||||
| C、4 | ||||
| D、3 |
设x∈R,向量
=(x,1),
=(1,-2),且
⊥
,则|
+
|=( )
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、2
| ||
D、
|
双曲线
-
=1的焦点坐标是( )
| x2 |
| 36 |
| y2 |
| 64 |
| A、(0,-10),(0,10) | ||||
| B、(-10,0),(10,0) | ||||
C、(-2
| ||||
D、(0,-2
|
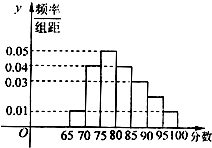 如图为某校语言类专业N名毕业生的综合测评成绩(百分制)分布直方图,已知80~90分数段的学员数为21人.
如图为某校语言类专业N名毕业生的综合测评成绩(百分制)分布直方图,已知80~90分数段的学员数为21人.