题目内容
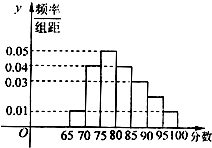 如图为某校语言类专业N名毕业生的综合测评成绩(百分制)分布直方图,已知80~90分数段的学员数为21人.
如图为某校语言类专业N名毕业生的综合测评成绩(百分制)分布直方图,已知80~90分数段的学员数为21人.(Ⅰ)求该专业毕业总人数N和90~95分数段内的人数n;
(Ⅱ)现欲将90~95分数段内的n名人分配到几所学校,从中安排2人到甲学校去,若n人中仅有两名男生,求安排结果至少有一名男生的概率.
考点:列举法计算基本事件数及事件发生的概率,频率分布直方图
专题:概率与统计
分析:(Ⅰ)根据频率分布直方图,先求出80~90分数段频率,即可求出N,再用1减去成绩落在其它区间上的频率,即得成绩落在90~95上的频率,继而期初该段的人数
(Ⅱ)一一列举出所有的基本事件,再找到满足条件的基本事件,根据概率公式计算即可
(Ⅱ)一一列举出所有的基本事件,再找到满足条件的基本事件,根据概率公式计算即可
解答:
解:(Ⅰ)80~90分数段频率为P1=(0.04+0.03)×5=0.35,
此分数段的学员总数为21人所以毕业生,
的总人数N为N=
=60,
90~95分数段内的人数频率为P1=1-(0.01+0.04+0.05+0.04+0.03+0.01)×5=0.1
所以90~95分数段内的人数n=60×0.1=6,
(Ⅱ) 90~95分数段内的6人中有两名男生,4名女生
设男生为1,2;女生为3,4,5,6,设安排结果中至少有一名男生为事件A
从中取两名毕业生的所有情况(基本事件空间)为12,13,14,15,16,23,24,25,26,34,35,36,45,46,56共15种组合方式,
每种组合发生的可能性是相同的,其中,至少有一名男生的种数为12,13,14,15,16,23,24,25,26共9种
所以,P(A)=
=
此分数段的学员总数为21人所以毕业生,
的总人数N为N=
| 21 |
| 0.35 |
90~95分数段内的人数频率为P1=1-(0.01+0.04+0.05+0.04+0.03+0.01)×5=0.1
所以90~95分数段内的人数n=60×0.1=6,
(Ⅱ) 90~95分数段内的6人中有两名男生,4名女生
设男生为1,2;女生为3,4,5,6,设安排结果中至少有一名男生为事件A
从中取两名毕业生的所有情况(基本事件空间)为12,13,14,15,16,23,24,25,26,34,35,36,45,46,56共15种组合方式,
每种组合发生的可能性是相同的,其中,至少有一名男生的种数为12,13,14,15,16,23,24,25,26共9种
所以,P(A)=
| 9 |
| 15 |
| 3 |
| 5 |
点评:本题主要考查频率分布直方图、等可能事件的概率,属基础题.

练习册系列答案
相关题目
已知双曲线C:
-
=1(a>0,b>0)的两条渐近线与抛物线y2=4x的准线分别交于A.,B两点,O为坐标原点,若△AOB的面积为
,则双曲线C的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| A、2 | ||||
B、
| ||||
C、
| ||||
D、
|
如图所示程序框图,算法流程图的输出结果是( )


| A、0 | B、B-1 | C、-2 | D、-3 |
如图是一容量为100的样本的重量的频率分布直方图,则由图可估计样本的平均重量为( )


| A、10 | B、11 | C、12 | D、13 |
双曲线
-
=1的离心率e=( )
| x2 |
| 4 |
| y2 |
| 5 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设a,b,c∈R,且a>b,则( )
A、(
| ||||
B、
| ||||
| C、a2>b2 | ||||
| D、a3>b3 |