题目内容
2014年春晚过后,为了研究演员上春晚次数与受关注度的关系,某网站对其中一位经常上春晚的演员上春晚次数与受关注度进行了统计,得到如下数据:
(Ⅰ)若该演员的粉丝数量y与上春晚次数x满足线性回归方程,试求回归方程
=
x+
,并就此分析,该演员上春晚12次时的粉丝数;
(Ⅱ)若用
=(i=1,2,3,4,5)表示统计数据时粉丝的“即时均值”(精确到整数)
(1)求这5次统计数据时粉丝的“即时均值”的方差;
(2)从“即时均值”中任选3组,求这三组数据之和不超过20的概率.参考公式:
=
=
,
=
-
.
| 上春晚次数x(单位:次) | 2 | 4 | 6 | 8 | 10 |
| 粉丝数量y(单位:万人) | 10 | 20 | 40 | 80 | 100 |
 |
| y |
 |
| b |
 |
| a |
(Ⅱ)若用
| yi |
| xi |
(1)求这5次统计数据时粉丝的“即时均值”的方差;
(2)从“即时均值”中任选3组,求这三组数据之和不超过20的概率.参考公式:
 |
| b |
| |||||||
|
| |||||||
|
 |
| a |
. |
| y |
 |
| b |
. |
| x |
考点:线性回归方程
专题:应用题,概率与统计
分析:(Ⅰ)利用公式求出
、
,可得回归方程
=
x+
,从而预测该演员上春晚12次时的粉丝数;
(Ⅱ)(1)计算出这5次统计数据,粉丝的“即时均值”,平均数,可得“即时均值”的方差;
(2)确定从5组“即时均值”任选3组、三组数据之和不超过20的基本事件数,即可求出概率.
 |
| b |
 |
| a |
 |
| y |
 |
| b |
 |
| a |
(Ⅱ)(1)计算出这5次统计数据,粉丝的“即时均值”,平均数,可得“即时均值”的方差;
(2)确定从5组“即时均值”任选3组、三组数据之和不超过20的基本事件数,即可求出概率.
解答:
解:(Ⅰ)由题意可知,
xiyi=1980,
xi2=220,
=
(2+4+6+8+10)=6,
=
(10+20+40+8+100)=50,
∴
=
=12,
∴
=50-12×6=-22,
∴
=12x-22
当x=12时,
=12×12-22=122,
即该演员上春晚12次时的粉丝数约为122万人.
(Ⅱ)(1)这5次统计数据,粉丝的“即时均值”分别为5,5,7,10,10,平均数为7.4,
方差
[2(5-7.4)2+(7-7.4)2+2(10-7.4)2]=5.04;
(2)从5组“即时均值”任选3组,共有
=10种情况,其中三组数据之和不超过20为(5,5,7),(5,5,10),(5,5,10)共3种情况,
∴所求概率为P=
.
| 5 |
 |
| i=1 |
| 5 |
 |
| i=1 |
. |
| x |
| 1 |
| 5 |
. |
| y |
| 1 |
| 5 |
∴
 |
| b |
| 1980-5•6•50 |
| 220-5•62 |
∴
 |
| a |
∴
 |
| y |
当x=12时,
 |
| y |
即该演员上春晚12次时的粉丝数约为122万人.
(Ⅱ)(1)这5次统计数据,粉丝的“即时均值”分别为5,5,7,10,10,平均数为7.4,
方差
| 1 |
| 5 |
(2)从5组“即时均值”任选3组,共有
| C | 3 5 |
∴所求概率为P=
| 3 |
| 10 |
点评:本题考查线性回归方程,考查概率知识,考查学生的计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知α,β表示两个相交的平面,直线l在平面α内且不是平面α,β的交线,则“l⊥β”是“α⊥β”的( )
| A、充分条件 |
| B、必要条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
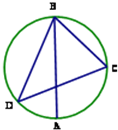 圆形广场的有南北两个大门在中轴线上,东、西各有一栋建筑物与北门的距离分别为30米和40米,且以北门为顶点(视大门和建筑物为点)的角为60°,求广场的直径(保留两位小数).
圆形广场的有南北两个大门在中轴线上,东、西各有一栋建筑物与北门的距离分别为30米和40米,且以北门为顶点(视大门和建筑物为点)的角为60°,求广场的直径(保留两位小数).