题目内容
如果（
+2x）11=a0+a1x+a2x2+…+a11x11，那么（a1+a3+a5+…+a11）2-（a0+a2+a4+…+a10）2的值是（ ）
| 3 |
| A、-1 | B、0 | C、3 | D、1 |
考点：二项式系数的性质
专题：二项式定理
分析：在所给的等式中，分别令x=1、x=-1，共得到2个等式，再把这两个等式相乘，即得所求．
解答：
解：在（
+2x）11=a0+a1x+a2x2+…+a11x11中，
令x=1可得 （
+2）11=a0+a1+a2+…+a11 ①，
令x=-1可得（
-2）11=a0-a1+a2+…-a11 ②，
①×②可得（a0+a2+a4+…+a10）2-（a1+a3+a5+…+a11）2 =（
+2）11 •（
-2）11 =-1，
∴（a1+a3+a5+…+a11）2-（a0+a2+a4+…+a10）2=1，
故选：D．
| 3 |
令x=1可得 （
| 3 |
令x=-1可得（
| 3 |
①×②可得（a0+a2+a4+…+a10）2-（a1+a3+a5+…+a11）2 =（
| 3 |
| 3 |
∴（a1+a3+a5+…+a11）2-（a0+a2+a4+…+a10）2=1，
故选：D．
点评：本题主要考查二项式定理的应用，在二项展开式中，通过给变量赋值，求得某些项的系数和，是一种简单有效的方法，属于中档题．
练习册系列答案
名师金手指领衔课时系列答案
相关题目
函数f（x）=2x-4+lnx的零点一定位于下列哪个区间（ ）
| A、（1，2） |
| B、（2，3） |
| C、（3，4） |
| D、（4，5） |
有关函数单调性的叙述中，正确的是（ ）
A、y=-
| ||
B、y=
| ||
| C、y=-3x2-6x的减区间为[-1，+∞） | ||
| D、y=ax+3在（-∞，+∞）上必为增函数 |
已知a1=1，如图给出程序框图，当k=5时，输出的S=（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
圆x2+y2+2x-4y=0的圆心坐标为（ ）
| A、（-1，2） |
| B、（-1，-2） |
| C、（1，-2） |
| D、（1，2） |
已知f（x）=
，则下列叙述中不正确的一项是（ ）
|
A、 f（x-1）的图象 |
B、 |f（x）|的图象 |
C、 f（-x）的图象 |
D、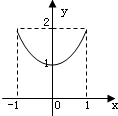 f（|x|）的图象 |
函数y=sinx+
cosx的最大值是（ ）
| 3 |
| A、1 | ||
B、
| ||
C、
| ||
| D、2 |
原点为圆心，直径为6的圆的方程是（ ）
| A、x2+y2=1 |
| B、x2+y2=3 |
| C、x2+y2=9 |
| D、x2+y2=36 |
