题目内容
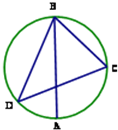圆形广场的有南北两个大门在中轴线上，东、西各有一栋建筑物与北门的距离分别为30米和40米，且以北门为顶点（视大门和建筑物为点）的角为60°，求广场的直径（保留两位小数）．考点：解三角形的实际应用
专题：应用题,解三角形
分析：设南、北门分别为点A、B，东、西建筑物分别为点C、D，在△BCD中，利用余弦定理，求出CD，再利用正弦定理求出广场直径．
解答：
解：
设南、北门分别为点A、B，东、西建筑物分别为点C、D．
在△BCD中，CD=
=
．（5分）
由于AB为△BCD的外接圆直径，
所以AB=
=
≈41.63米．
所以广场直径约为41.63米．（12分）
设南、北门分别为点A、B，东、西建筑物分别为点C、D．在△BCD中，CD=
| 302+402-2•30•40•cos60° |
| 1300 |
由于AB为△BCD的外接圆直径，
所以AB=
| CD |
| sin60° |
20
| ||
| 3 |
所以广场直径约为41.63米．（12分）
点评：本题考查解三角形的实际应用，考查余弦定理、正弦定理的运用，属于中档题．
练习册系列答案
黄冈创优卷系列答案
相关题目
已知a1=1，如图给出程序框图，当k=5时，输出的S=（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
原点为圆心，直径为6的圆的方程是（ ）
| A、x2+y2=1 |
| B、x2+y2=3 |
| C、x2+y2=9 |
| D、x2+y2=36 |
在等比数列{an}中，a1=27，q=-
，则S3=（ ）
| 1 |
| 3 |
| A、21 | B、22 | C、12 | D、28 |
