题目内容

某公司使用水下探测器寻找坠落于海底P处且不断发出电子信号的一个物件．工程师建立的坐标系如下：取原点为工作母船位置，x轴为海平面，y轴为垂直向上方向，单位长度为一百米．探测器在水下沿一条直线完成了一次探测任务，工程师分析数据后发现：探测器在B（8，-5）处收到的坠落物电子信号最强，又在A（5，-4）处探测器到坠落物的距离恰为探测器到母船距离的2倍．求该坠落物P的位置坐标．
考点：直线和圆的方程的应用
专题：综合题,直线与圆
分析：求出直线AB的方程，以A为圆心，|PA|为半径的圆的方程，联立求出交点坐标即可．
解答： 解：由题意，直线AB的方程为
y+5
-4+5
=
x-8
5-8
，即x=-3y-7，
∵|OA|=
25+16
=
41
，
∴|PA|=2
41
，
∴以A为圆心，|PA|为半径的圆的方程为（x-5）2+（y+4）2=164，
x=-3y-7代入可得（-3y-7-5）2+（y+4）2=164，
∴5y2+40y-12=0
∴y=
-20±2
115
5
，
∴x=
-115±6
115
5
，
∴该坠落物P的位置坐标为（
-115±6
115
5
，
-20±2
115
5
）．
点评：本题考查利用圆的知识解决实际问题，考查学生分析解决问题的能力，确定圆的方程是关键．
练习册系列答案
相关题目
已知f（x）=
x+1，x∈[-1，0)
x2+1．x∈[0，1]
，则下列叙述中不正确的一项是（　　）
A、
f（x-1）的图象
B、
|f（x）|的图象
C、
f（-x）的图象
D、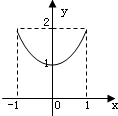
f（|x|）的图象
在等比数列{an}中，a1=27，q=-
1
3
，则S3=（　　）
A、21B、22C、12D、28
求函数y=3sin（2x+
π
3
）的最大值和最小值及相应的x值的范围．
2014年春晚过后，为了研究演员上春晚次数与受关注度的关系，某网站对其中一位经常上春晚的演员上春晚次数与受关注度进行了统计，得到如下数据：
上春晚次数x（单位：次） 2 4 6 8 10
粉丝数量y（单位：万人） 10 20 40 80 100
（Ⅰ）若该演员的粉丝数量y与上春晚次数x满足线性回归方程，试求回归方程
y
=
b
x+
a
，并就此分析，该演员上春晚12次时的粉丝数；
（Ⅱ）若用
yi
xi
=（i=1，2，3，4，5）表示统计数据时粉丝的“即时均值”（精确到整数）
（1）求这5次统计数据时粉丝的“即时均值”的方差；
（2）从“即时均值”中任选3组，求这三组数据之和不超过20的概率．参考公式：
b
=
n
i=1
(xi-
.
x
)(yi-
.
y
)
n
i=1
(xi-
.
x
)2
=
n
i=1
xiyi-n
.
xy
n
i=1
x
2
i
-n
.
x
2
，
a
=
.
y
-
b
.
x
．
已知
a
=（1，cosx），
b
=（sin2x，2cosx），且f（x）=
a
•
b
-1．
（1）求函数y=f（x），x∈[0，π]的单调增区间；
（2）证明：无论m为何值，直线4x-y+m=0与函数y=f（x）的图象不相切．
在△ABC中，角A、B、c的时边长分别为a、b、c，已知
3
sinB-cosB=l，且b=1．
（Ⅰ）若A=
5π
12
，求c的值；
（Ⅱ）设AC边上的高为h，求h的最大值．
已知数列{an}的通项公式为an=3n-1+1，则a1C
 
0
n
+a2C
 
1
n
+a3C
 
2
n
+…+an+1C
 
n
n
的最简表达式为
 
．
己知抛物线的参数方程为
x=4t2
y=4t
（t为参数），焦点为F，准线为l1，直线l2的参数方程为
x=1+
1
2
m
y=
3
2
m
（m为参数）．若直线l2与抛物线在x轴上方的部分相交于点A，是AM⊥l1，垂足为M，则△AMF的面积是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网