题目内容
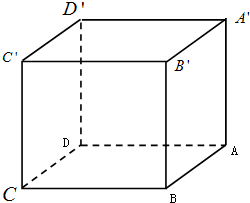已知长方体ABCD-A′B′C′D′中，AB=2| 3 |
| 3 |
（1）BC与A′C′所成的角是多少？
（2）AA′与BC′所成的角是多少？
考点：异面直线及其所成的角
专题：空间位置关系与距离
分析：①长方体ABCD-A1B1C1D1中，由A1C1∥AC，知∠BCA是BC和A1C1所成的角，由此能求出BC和A1C1所成的角．
②由AA1⊥平面A1B1C1D1，B1C1?平面A1B1C1D1，能求出AA1和B1C1所成的角．
②由AA1⊥平面A1B1C1D1，B1C1?平面A1B1C1D1，能求出AA1和B1C1所成的角．
解答：
解：（1）∵BC∥B'C'，
∴∠B'C'A'就是BC与A'C'所成的角；
∵长方体ABCD-A′B′C′D′中，AB=2
，AD=2
，AA′=2，
∴∠B'C'A'=45°；
∴BC与A′C′所成的角是45°；
（2）∵AA'∥BB'．
∴∠B'BC'就是AA'与BC'所成的角；
∵长方体ABCD-A′B′C′D′中，AB=2
，AD=2
，AA′=2，
∴tan∠B'BC'=
=
=
，
∴∠B'BC'=60°，
∴AA′与BC′所成的角是60°．
∴∠B'C'A'就是BC与A'C'所成的角；
∵长方体ABCD-A′B′C′D′中，AB=2
| 3 |
| 3 |
∴∠B'C'A'=45°；
∴BC与A′C′所成的角是45°；
（2）∵AA'∥BB'．
∴∠B'BC'就是AA'与BC'所成的角；
∵长方体ABCD-A′B′C′D′中，AB=2
| 3 |
| 3 |
∴tan∠B'BC'=
| B′C′ |
| BB′ |
2
| ||
| 2 |
| 3 |
∴∠B'BC'=60°，
∴AA′与BC′所成的角是60°．
点评：本题考查异面直线所成角的大小的求法，关键是将空间角转为平面角解答，注意等价转化思想的合理运用．
练习册系列答案
相关题目
已知函数f（x）=3x，且f（a+2）=18，g（x）=3ax-4x的定义域为区间[0，1]．
（1）求g（x）的解析式；
（2）求g（x）的单调区间，确定其增减性并试用定义证明；
（3）求g（x）的值域．
（1）求g（x）的解析式；
（2）求g（x）的单调区间，确定其增减性并试用定义证明；
（3）求g（x）的值域．
若函数f（x）=kx-lnx在区间（1，+∞）单调递增，则k的取值范围是（ ）
| A、（-∞，-2] |
| B、（-∞，-1] |
| C、[2，+∞） |
| D、[1，+∞） |
下列命题的说法错误的是（ ）
| A、命题“若x2-3x+2=0，则 x=1”的逆否命题为：“若x≠1，则x2-3x+2≠0” |
| B、若p∧q为假命题，则p，q均为假命题 |
| C、“x=1”是“x2-3x+2=0”的充分不必要条件 |
| D、对于命题p：?x∈R，x2+x+1＞0，则￢p：?x∈R，x2+x+1≤0 |
如图，由三个小立方体搭成的几何体的俯视图是（ ）
A、 |
B、 |
C、 |
D、 |
若一个几何体的主视图和左视图是边长为2的等边三角形，俯视图是一个圆，则这个几何体的体积是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
| D、不能确定 |