题目内容
若函数f（x）=kx-lnx在区间（1，+∞）单调递增，则k的取值范围是（ ）
| A、（-∞，-2] |
| B、（-∞，-1] |
| C、[2，+∞） |
| D、[1，+∞） |
考点：利用导数研究函数的单调性
专题：导数的综合应用
分析：f′（x）=k-
，由于函数f（x）=kx-lnx在区间（1，+∞）单调递增，可得f′（x）≥0在区间（1，+∞）上恒成立．
解出即可．
| 1 |
| x |
解出即可．
解答：
解：f′（x）=k-
，
∵函数f（x）=kx-lnx在区间（1，+∞）单调递增，
∴f′（x）≥0在区间（1，+∞）上恒成立．
∴k≥
，
而y=
在区间（1，+∞）上单调递减，
∴k≥1．
∴k的取值范围是[1，+∞）．
故选：D．
| 1 |
| x |
∵函数f（x）=kx-lnx在区间（1，+∞）单调递增，
∴f′（x）≥0在区间（1，+∞）上恒成立．
∴k≥
| 1 |
| x |
而y=
| 1 |
| x |
∴k≥1．
∴k的取值范围是[1，+∞）．
故选：D．
点评：本题查克拉利用导数研究函数的单调性、恒成立问题的等价转化方法，属于基础题．
练习册系列答案
相关题目
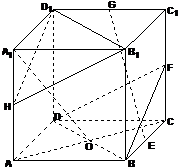正方体ABCD-A1B1C1D1中，F，H分别为棱CC1，AA1的中点，O为AC与BD的交点．
如图：AB是⊙O的直径，PA垂直于⊙O所在的平面，C是圆周上不同于A，B的任意一点，求证：平面PAC⊥平面PBC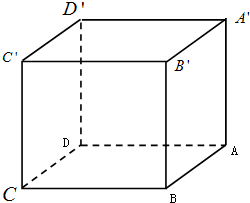．已知sin（π-x）=2cosx，则sin2x+1=（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
已知长方体ABCD-A′B′C′D′中，AB=2设△ABC的内角A、B、C所对边的长分别为a、b、c，拓a=2，b=
，B=
，则△ABC的面积为（ ）
| 3 |
| π |
| 3 |
A、
| ||||
B、
| ||||
| C、1 | ||||
D、
|