题目内容
函数f(x)=cos2xcos
-2sinxcosxsin
的递增区间是 .
| π |
| 5 |
| 6π |
| 5 |
考点:三角函数中的恒等变换应用
专题:三角函数的图像与性质
分析:首先将解析式化简为一个角的一个三角函数的形式,然后利用三角函数的性质解答.
解答:
解:f(x)=cos2xcos
-2sinxcosxsin
=cos2xcos
+sin2xsin
=cos(2x-
);
因为余弦函数y=cosx的单调递增区间为[2kπ-π,2kπ],
所以2kπ-π≤2x-
≤2kπ,
所以kπ-
≤x≤kπ+
,k∈Z.
所以f(x)=cos2xcos
-2sinxcosxsin
的单调递增区间为[kπ-
,kπ+
],k∈Z.
| π |
| 5 |
| 6π |
| 5 |
| π |
| 5 |
| π |
| 5 |
=cos(2x-
| π |
| 5 |
因为余弦函数y=cosx的单调递增区间为[2kπ-π,2kπ],
所以2kπ-π≤2x-
| π |
| 5 |
所以kπ-
| 2π |
| 5 |
| π |
| 10 |
所以f(x)=cos2xcos
| π |
| 5 |
| 6π |
| 5 |
| 2π |
| 5 |
| π |
| 10 |
点评:本题考查了三角函数式的化简以及三角函数的性质,关键是正确将解析式化简为一个角的以后三角函数的形式.再求单调区间.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
已知sin(π-x)=2cosx,则sin2x+1=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 在平面四边形ABCD中,AB=3,BC=4,∠ABC=90°,△ACD是正三角形,则
在平面四边形ABCD中,AB=3,BC=4,∠ABC=90°,△ACD是正三角形,则| AC |
| BD |
| A、-2 | ||
| B、2 | ||
C、
| ||
D、-
|
已知向量
=(0,6),
=(x,y),
与
-
的夹角为
,则|
|的最大值是( )
| a |
| b |
| b |
| a |
| b |
| 2π |
| 3 |
| b |
| A、6 | ||
B、4
| ||
C、6
| ||
| D、12 |
已知α是第二象限角,直线sinαx+tanαy+cosα=0不经过( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
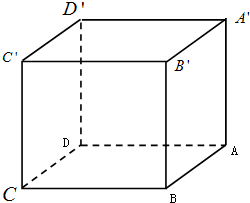 已知长方体ABCD-A′B′C′D′中,AB=2
已知长方体ABCD-A′B′C′D′中,AB=2