题目内容
若一个几何体的主视图和左视图是边长为2的等边三角形,俯视图是一个圆,则这个几何体的体积是( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、不能确定 |
考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:根据几何体的三视图得出该几何体是圆锥,求出圆锥的体积即可.
解答:
解:根据几何体的三视图知,
该几何体是底面直径为2,母线长为2的圆锥,
∴这个圆锥的体积是
V圆锥=
S底面h
=
•π(
)2•
=
.
故选:B.
该几何体是底面直径为2,母线长为2的圆锥,
∴这个圆锥的体积是
V圆锥=
| 1 |
| 3 |
=
| 1 |
| 3 |
| 2 |
| 2 |
22-(
|
=
| ||
| 3 |
故选:B.
点评:本题考查了空间几何体的三视图的应用问题,解题时应根据三视图得出该几何体是什么图形,是基础题.

练习册系列答案
相关题目
已知向量
=(0,6),
=(x,y),
与
-
的夹角为
,则|
|的最大值是( )
| a |
| b |
| b |
| a |
| b |
| 2π |
| 3 |
| b |
| A、6 | ||
B、4
| ||
C、6
| ||
| D、12 |
在地面上某处测的山峰的仰角为θ,对着山峰在地面上前进600M后,测得仰角为2θ,继续前进200
m后有测得仰角为4θ,则山的高度为( )
| 3 |
| A、200 | B、300 |
| C、400 | D、500 |
设△ABC的内角A、B、C所对边的长分别为a、b、c,拓a=2,b=
,B=
,则△ABC的面积为( )
| 3 |
| π |
| 3 |
A、
| ||||
B、
| ||||
| C、1 | ||||
D、
|
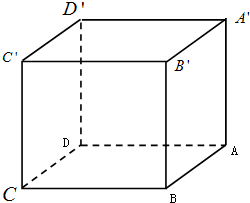 已知长方体ABCD-A′B′C′D′中,AB=2
已知长方体ABCD-A′B′C′D′中,AB=2