题目内容
已知函数f(x)=3x,且f(a+2)=18,g(x)=3ax-4x的定义域为区间[0,1].
(1)求g(x)的解析式;
(2)求g(x)的单调区间,确定其增减性并试用定义证明;
(3)求g(x)的值域.
(1)求g(x)的解析式;
(2)求g(x)的单调区间,确定其增减性并试用定义证明;
(3)求g(x)的值域.
考点:指数函数的图像与性质
专题:函数的性质及应用
分析:(1)由f(a+2)=18可得3a+2=18,求得3a=2,可得g(x)的解析式,
(2)转化设t=2x,1≤t≤2,则y=k(t)=t-t2,1≤t≤2,对称轴t=
,写出单调区间,运用定义证明.
(3)根据函数的单调性,求解即可得出值域.
(2)转化设t=2x,1≤t≤2,则y=k(t)=t-t2,1≤t≤2,对称轴t=
| 1 |
| 2 |
(3)根据函数的单调性,求解即可得出值域.
解答:
解:(1)∵f(x)=3x,f(a+2)=18,∴3a+2=18,得3a=2,
∴g(x)=2x-4x,x∈[0,1].
(2)∵g(x)=2x-4x =2x-(2x)2,x∈[0,1],
设t=2x,1≤t≤2,则y=k(t)=t-t2,1≤t≤2,对称轴t=
,
∴t∈[1,2]单调递减,
∵t=2x为[0,1]上的增函数,
∴g(x)在[0,1]上为减函数,
证明:∵设0≤x1<x2≤1,1≤t1<t2≤2,t1-t2<0,1-t1-t2<0
∴g(x1)-g(x2)=k(t1)-k(t2)=(t1-t2)(1-t1-t2)>0,
即k(t1)>k(t2),
g(x1)>g(x2),
∴g(x)在[0,1]上为减函数,
(3)∵g(x)=2x-4x,x∈[0,1]上为减函数,
∴g(0)=0,g(1)=-2,
∴g(x)的值域:[-2,0]
∴g(x)=2x-4x,x∈[0,1].
(2)∵g(x)=2x-4x =2x-(2x)2,x∈[0,1],
设t=2x,1≤t≤2,则y=k(t)=t-t2,1≤t≤2,对称轴t=
| 1 |
| 2 |
∴t∈[1,2]单调递减,
∵t=2x为[0,1]上的增函数,
∴g(x)在[0,1]上为减函数,
证明:∵设0≤x1<x2≤1,1≤t1<t2≤2,t1-t2<0,1-t1-t2<0
∴g(x1)-g(x2)=k(t1)-k(t2)=(t1-t2)(1-t1-t2)>0,
即k(t1)>k(t2),
g(x1)>g(x2),
∴g(x)在[0,1]上为减函数,
(3)∵g(x)=2x-4x,x∈[0,1]上为减函数,
∴g(0)=0,g(1)=-2,
∴g(x)的值域:[-2,0]
点评:本题综合考察了函数的性质,运用求解最大值,最小值,难度不大,容易出错,做题要认真仔细.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设f(x)=
,则f(2012)=( )
|
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
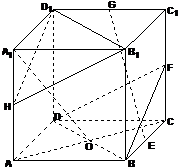 正方体ABCD-A1B1C1D1中,F,H分别为棱CC1,AA1的中点,O为AC与BD的交点.
正方体ABCD-A1B1C1D1中,F,H分别为棱CC1,AA1的中点,O为AC与BD的交点. 如图:已知PA⊥平面ABC,AB是⊙O的直径,C是圆上的任意一点,求证:PC⊥BC.
如图:已知PA⊥平面ABC,AB是⊙O的直径,C是圆上的任意一点,求证:PC⊥BC.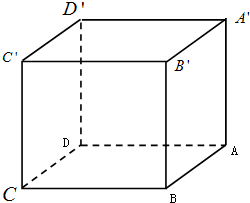 已知长方体ABCD-A′B′C′D′中,AB=2
已知长方体ABCD-A′B′C′D′中,AB=2