题目内容
已知函数y=f(x)的定义域为R,且对任意a,b∈R,都有f(a+b)=f(a)+f(b),且当x>0时,f(x)<0恒成立,
(1)求证:函数y=f(x)是奇函数;
(2)判断函数y=f(x)是R上的增函数还是减函数,并证明你的结论.
(1)求证:函数y=f(x)是奇函数;
(2)判断函数y=f(x)是R上的增函数还是减函数,并证明你的结论.
考点:抽象函数及其应用
专题:函数的性质及应用
分析:(1)令a=b=0,则可得f(0)=0;再令a=x,b=-x,即可证明f(x)是奇函数.
(2)设x1>x2,由已知可得f(x1-x2)<0,再利用f(a+b)=f(a)+f(b)及减函数的定义即可证明.
(2)设x1>x2,由已知可得f(x1-x2)<0,再利用f(a+b)=f(a)+f(b)及减函数的定义即可证明.
解答:
证明:(1)由f(a+b)=f(a)+f(b),、
令a=b=0,得f(0)=f(0)+f(0),
∴f(0)=0,
再令a=x,b=-x,
得f(x-x)=f(x)+f(-x)
即f(x)+f(-x)=f(0)=0,
∴f(-x)=-f(x),
即函数y=f(x)是奇函数.
(2)函数y=f(x)为减函数,理由如下
设x1>x2,则x1-x2>0,
∵x>0时,f(x)<0,
∴f(x1-x2)<0,
∴f(x1)=f(x1-x2+x2)=f(x1-x2)+f(x2)<f(x2)
∴函数y=f(x)是R上的减函数;
令a=b=0,得f(0)=f(0)+f(0),
∴f(0)=0,
再令a=x,b=-x,
得f(x-x)=f(x)+f(-x)
即f(x)+f(-x)=f(0)=0,
∴f(-x)=-f(x),
即函数y=f(x)是奇函数.
(2)函数y=f(x)为减函数,理由如下
设x1>x2,则x1-x2>0,
∵x>0时,f(x)<0,
∴f(x1-x2)<0,
∴f(x1)=f(x1-x2+x2)=f(x1-x2)+f(x2)<f(x2)
∴函数y=f(x)是R上的减函数;
点评:本题考查了抽象函数的奇偶性和单调性,深刻理解函数奇偶性和单调性的定义及充分利用已知条件是解决问题的关键.

练习册系列答案
相关题目
设△ABC的内角A、B、C所对边的长分别为a、b、c,拓a=2,b=
,B=
,则△ABC的面积为( )
| 3 |
| π |
| 3 |
A、
| ||||
B、
| ||||
| C、1 | ||||
D、
|
已知α是第二象限角,直线sinαx+tanαy+cosα=0不经过( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
若正数a、b满足ab=a+b+3,则a+b的取值范围是( )
| A、[9,+∞) |
| B、[6,+∞) |
| C、(0,9] |
| D、(0,6) |
已知集合M={1,3,5},N={1},则下列关系式正确的是( )
| A、N∈M | B、N∉M |
| C、N=M | D、N⊆M |
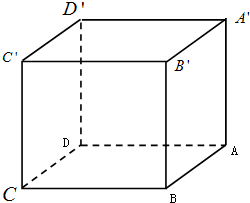 已知长方体ABCD-A′B′C′D′中,AB=2
已知长方体ABCD-A′B′C′D′中,AB=2