题目内容
17.已知点P在抛物线y2=4x上,那么点P到点Q(2,-1)的距离与点P到抛物线焦点距离之和取得最小值时,点P的坐标为( )| A. | ($\frac{1}{4}$,-1) | B. | ($\frac{1}{4}$,1) | C. | ($\frac{1}{2}$,-1) | D. | ($\frac{1}{2}$,1) |
分析 先根据抛物线方程求出焦点坐标,再由抛物线的性质知:当P,Q和焦点三点共线且点P在中间的时候距离之和最小,进而先求出纵坐标的值,代入到抛物线中可求得横坐标的值从而得到答案.
解答  解:∵y2=4x
解:∵y2=4x
∴p=2,焦点坐标为(1,0)
过M作准线的垂线于M,由PF=PM,
依题意可知当P,Q和M三点共线且点P在中间的时候,
距离之和最小如图,
故P的纵坐标为-1,然后代入抛物线方程求得x=$\frac{1}{4}$,
故选A.
点评 本题主要考查抛物线的基本性质,考查抛物线的定义,属基础题.

练习册系列答案
相关题目
8.复数$\frac{{i({-6+i})}}{{|{3-4i}|}}$的实部与虚部之差为( )
| A. | -1 | B. | 1 | C. | $-\frac{7}{5}$ | D. | $\frac{7}{5}$ |
5.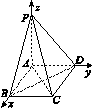 如图,已知四边形ABCD为矩形,PA⊥平面ABCD,连接AC,BD,PB,PC,PD,则下列各组向量中,数量积不一定为零的是( )
如图,已知四边形ABCD为矩形,PA⊥平面ABCD,连接AC,BD,PB,PC,PD,则下列各组向量中,数量积不一定为零的是( )
 如图,已知四边形ABCD为矩形,PA⊥平面ABCD,连接AC,BD,PB,PC,PD,则下列各组向量中,数量积不一定为零的是( )
如图,已知四边形ABCD为矩形,PA⊥平面ABCD,连接AC,BD,PB,PC,PD,则下列各组向量中,数量积不一定为零的是( )| A. | $\overrightarrow{PC}$与$\overrightarrow{BD}$ | B. | $\overrightarrow{DA}$与$\overrightarrow{PB}$ | C. | $\overrightarrow{PD}$与$\overrightarrow{AB}$ | D. | $\overrightarrow{PA}$与$\overrightarrow{CD}$ |
7.sin30°+tan240°的值是( )
| A. | -$\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$+$\sqrt{3}$ | D. | $\frac{1}{2}$+$\sqrt{3}$ |