题目内容
5.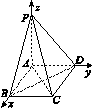 如图,已知四边形ABCD为矩形,PA⊥平面ABCD,连接AC,BD,PB,PC,PD,则下列各组向量中,数量积不一定为零的是( )
如图,已知四边形ABCD为矩形,PA⊥平面ABCD,连接AC,BD,PB,PC,PD,则下列各组向量中,数量积不一定为零的是( )| A. | $\overrightarrow{PC}$与$\overrightarrow{BD}$ | B. | $\overrightarrow{DA}$与$\overrightarrow{PB}$ | C. | $\overrightarrow{PD}$与$\overrightarrow{AB}$ | D. | $\overrightarrow{PA}$与$\overrightarrow{CD}$ |
分析 根据题意,若空间非零向量的数量积为0,则这两个向量必然互相垂直.据此依次分析选项,判定所给的向量是否垂直,即可得答案.
解答 解:根据题意,依次分析选项:
对于A、PC与BD不一定垂直,即向量$\overrightarrow{PC}$、$\overrightarrow{BD}$不一定垂直,则向量$\overrightarrow{PC}$、$\overrightarrow{BD}$的数量积不一定为0,
对于B、根据题意,有PA⊥平面ABCD,则PA⊥AD,又由AD⊥AB,则有AD⊥平面PAB,进而有AD⊥PB,即向量$\overrightarrow{DA}$、$\overrightarrow{PB}$一定垂直,则向量$\overrightarrow{DA}$、$\overrightarrow{PB}$的数量积不一定为0,
对于C、根据题意,有PA⊥平面ABCD,则PA⊥AB,又由AD⊥AB,则有AB⊥平面PAD,进而有AB⊥PD,即向量$\overrightarrow{PD}$、$\overrightarrow{AB}$一定垂直,则向量$\overrightarrow{PD}$、$\overrightarrow{AB}$的数量积不一定为0,
对于D、根据题意,有PA⊥平面ABCD,则PA⊥CD,即向量$\overrightarrow{PA}$、$\overrightarrow{CD}$一定垂直,则向量$\overrightarrow{PA}$、$\overrightarrow{CD}$的数量积不一定为0,
故选:A.
点评 本题考查空间向量的数量积的运算,若空间非零向量的数量积为0,则这两个向量必然互相垂直.

练习册系列答案
相关题目
9.下列函数既是奇函数,又在区间(0,+∞)上是增函数的是( )
| A. | y=x-1 | B. | y=x2 | C. | y=lgx | D. | y=x3 |
10.已知集合M={-3,-2,-1},N={x|(x+2)(x-3)<0},则M∩N=( )
| A. | {-1} | B. | {-2,-1} | C. | {-2,-1} | D. | {-3,3} |
13.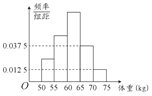 为了了解我校今年报考飞行员的学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,第2小组的频数为12,则报考飞行员的学生人数是( )
为了了解我校今年报考飞行员的学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,第2小组的频数为12,则报考飞行员的学生人数是( )
 为了了解我校今年报考飞行员的学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,第2小组的频数为12,则报考飞行员的学生人数是( )
为了了解我校今年报考飞行员的学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,第2小组的频数为12,则报考飞行员的学生人数是( )| A. | 50 | B. | 47 | C. | 48 | D. | 52 |
20.已知定义在R上的函数f(x)满足f(x)=f(4-x),且当x≥2时,f(x)=4x+2x-6,则f(x)在区间[0,4]上的最大值与最小值分别为( )
| A. | 266,14 | B. | 256,14 | C. | 256,-$\frac{21}{4}$ | D. | 266,-4 |
17.已知点P在抛物线y2=4x上,那么点P到点Q(2,-1)的距离与点P到抛物线焦点距离之和取得最小值时,点P的坐标为( )
| A. | ($\frac{1}{4}$,-1) | B. | ($\frac{1}{4}$,1) | C. | ($\frac{1}{2}$,-1) | D. | ($\frac{1}{2}$,1) |
14.设a=0.5${\;}^{\frac{1}{2}}$,b=0.9${\;}^{\frac{1}{2}}$,c=log50.3,则a,b,c的大小关系是( )
| A. | a>c>b | B. | c>a>b | C. | a>b>c | D. | b>a>c |
15.直线y=kx+1-2k与椭圆$\frac{x^2}{9}+\frac{y^2}{4}=1$的位置关系为( )
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 不确定 |