题目内容
2．在空间直角坐标系O-xyz中，有两点P（1，-2，3），M（2，0，4）则两点之间的距离为$\sqrt{6}$．分析 由空间两点间距离公式，直接求解即可得出结论．
解答 解：∵P（1，-2，3），M（2，0，4），
∴|PM|=$\sqrt{（2-1）^{2}+（0+2）^{2}+（4-3）^{2}}$=$\sqrt{6}$．
故答案为$\sqrt{6}$
点评 本题考查两点间距离公式的应用，考查学生的计算能力，比较基础．
练习册系列答案
孟建平小学滚动测试系列答案
黄冈天天练口算题卡系列答案
相关题目
6．对于R上可导的任意函数f（x），若a＞b＞1，且有（x-1）f′（x）≥0，则必有（ ）
| A． | f（a）+f（b）＜2 f（1） | B． | f（a）+f（b）≤2 f（1） | C． | f（a）+f（b）≥2 f（1） | D． | f（a）+f（b）＞2 f（1） |
13．
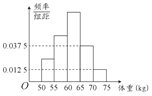为了了解我校今年报考飞行员的学生的体重情况，将所得的数据整理后，画出了频率分布直方图（如图），已知图中从左到右的前3个小组的频率之比为1：2：3，第2小组的频数为12，则报考飞行员的学生人数是（ ）
为了了解我校今年报考飞行员的学生的体重情况，将所得的数据整理后，画出了频率分布直方图（如图），已知图中从左到右的前3个小组的频率之比为1：2：3，第2小组的频数为12，则报考飞行员的学生人数是（ ）| A． | 50 | B． | 47 | C． | 48 | D． | 52 |
17．已知点P在抛物线y2=4x上，那么点P到点Q（2，-1）的距离与点P到抛物线焦点距离之和取得最小值时，点P的坐标为（ ）
| A． | （$\frac{1}{4}$，-1） | B． | （$\frac{1}{4}$，1） | C． | （$\frac{1}{2}$，-1） | D． | （$\frac{1}{2}$，1） |
14．设a=0.5${\;}^{\frac{1}{2}}$，b=0.9${\;}^{\frac{1}{2}}$，c=log50.3，则a，b，c的大小关系是（ ）
| A． | a＞c＞b | B． | c＞a＞b | C． | a＞b＞c | D． | b＞a＞c |
11．设函数$f（x）=x-\frac{1}{x}$，对任意x∈[1，+∞），f（mx）+mf（x）＜0恒成立，则实数m的取值范围是 （ ）
| A． | m＜-1或0＜m＜1 | B． | 0＜m＜1 | C． | m＜-1 | D． | -1＜m＜0 |
12．若$α∈（0，\frac{π}{2}）$，若$cos（α+\frac{π}{6}）=\frac{4}{5}$，则$sin（2α+\frac{π}{3}）$的值为（ ）
| A． | $\frac{12}{25}$ | B． | $\frac{24}{25}$ | C． | $-\frac{24}{25}$ | D． | $-\frac{12}{25}$ |