题目内容
若集合A={x|x2-[2a+(a2+1)]x+2a(a2+1)≤0},B={x|(x-2[x-(3a+1)]≤0},当实数a为何值时,A⊆B.
考点:集合的包含关系判断及应用
专题:集合
分析:本题是一元二次不等式和集合包含关系结合的题目,需要分类讨论,求出a的取值范围.
解答:
解:∵集合A={x|x2-[2a+(a2+1)]x+2a(a2+1)≤0},
∴A={x|2a≤x≤a2+1},
∵B={x|(x-2[x-(3a+1)]≤0},
∴B={x|x≥6a+2},
若A⊆B.只需满足,6a+2≤2a
即a≤-
.
∴A={x|2a≤x≤a2+1},
∵B={x|(x-2[x-(3a+1)]≤0},
∴B={x|x≥6a+2},
若A⊆B.只需满足,6a+2≤2a
即a≤-
| 1 |
| 2 |
点评:本题主要考查集合的基本运算,属于基础题.要正确判断两个集合间的关系,必须对集合的相关概念有深刻的理解,善于抓住代表元素,认清集合的特征

练习册系列答案
相关题目
某四棱锥的三视图如图所示,该四棱锥的体积为( )


| A、8 | B、16 | C、24 | D、32 |
“a=±2”是“直线ax-4y+1=0与直线ax+y+1=0互相垂直”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
某市组织一次高三调研考试,考试后统计的数学成绩服从正态分布,其密度函数f(x)=
e-
(x∈(-∞,+∞)),则下列命题不正确的是( )
| 1 | ||
|
| (x-90)2 |
| 400 |
| A、该市这次考试的数学平均成绩为90分 |
| B、分数在120分以上的人数与分数在60分以下的人数相同 |
| C、分数在110分以上的人数与分数在50分以下的人数相同 |
| D、该市这次考试的数学标准差为20 |
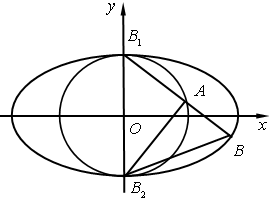 已知椭圆C1:
已知椭圆C1: 如图,如果你在海边沿着海岸线直线前行,请设计一种测量海中两个小岛A,B之间距离的方法.
如图,如果你在海边沿着海岸线直线前行,请设计一种测量海中两个小岛A,B之间距离的方法.