题目内容
若过点A(0,1)和B(4,m),并且与x轴相切的圆只有一个,求实数m的值和这圆的方程.
考点:直线与圆的位置关系
专题:直线与圆
分析:设出圆心的坐标,由圆心到A、B及x轴的距离相等列两式a2+(b-1)2=b2,(4-a)2+(m-b)2=b2,消去b后得关于a的方程,然后分二次项系数等于0和二次项系数不等于0时判别式等于0求解m的值,进一步求出a,b的值,则圆的方程可求.
解答:
解:∵圆过点A(0,1)和B(4,m),并且与x轴相切,
∴圆心必在AB的垂直平分线上,且圆心到A,B及x轴的距离相等,
设圆心为(a,b),则有:
a2+(b-1)2=b2 ①
(4-a)2+(m-b)2=b2 ②
联立①②消去b得:(1-m)a2-8a+m2-m+16=0 ③
∵过点A(0,1)和B(4,m),并且与x轴相切的圆只有一个,
∴方程③有唯一解,
当1-m=0,即m=1时方程有唯一解,把m=1代入③,得a=2,
把a=2代入①,得b=
.
∴圆的方程为:(x-2)2+(y-
)2=(
)2;
当1-m≠0时,需△=(-8)2-4(1-m)(m2-m+16)=4m3-8m2+68m=0,
解得:m=0.
把m=0代入③,得a=4,
把a=4代入①,得b=
.
∴圆的方程为:(x-4)2+(y-
)2=(
)2.
综上:当m=0时,相对应的圆的方程为:(x-4)2+(y-
)2=(
)2;
当m=1时,相对应的圆的方程为:(x-2)2+(y-
)2=(
)2.
∴圆心必在AB的垂直平分线上,且圆心到A,B及x轴的距离相等,
设圆心为(a,b),则有:
a2+(b-1)2=b2 ①
(4-a)2+(m-b)2=b2 ②
联立①②消去b得:(1-m)a2-8a+m2-m+16=0 ③
∵过点A(0,1)和B(4,m),并且与x轴相切的圆只有一个,
∴方程③有唯一解,
当1-m=0,即m=1时方程有唯一解,把m=1代入③,得a=2,
把a=2代入①,得b=
| 5 |
| 2 |
∴圆的方程为:(x-2)2+(y-
| 5 |
| 2 |
| 5 |
| 2 |
当1-m≠0时,需△=(-8)2-4(1-m)(m2-m+16)=4m3-8m2+68m=0,
解得:m=0.
把m=0代入③,得a=4,
把a=4代入①,得b=
| 17 |
| 2 |
∴圆的方程为:(x-4)2+(y-
| 17 |
| 2 |
| 17 |
| 2 |
综上:当m=0时,相对应的圆的方程为:(x-4)2+(y-
| 17 |
| 2 |
| 17 |
| 2 |
当m=1时,相对应的圆的方程为:(x-2)2+(y-
| 5 |
| 2 |
| 5 |
| 2 |
点评:本题考查了直线与圆的位置关系,考查了分类讨论的数学思想方法,明确方程(1-m)a2-8a+m2-m+16=0仅有一个实根的条件是解答此题的关键,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
| ∫ | 0 -2 |
| 4-x2 |
| A、4π | ||
| B、2π | ||
| C、π | ||
D、
|
要得到函数y=cos(2x+
)的图象,只需将y=cos2x的图象( )
| π |
| 4 |
A、向右平移
| ||
B、向左平移
| ||
C、向左平移
| ||
D、向右平移
|
下列不等式成立的是( )
| A、ex<x+1 | ||||
| B、lnx>x-1 | ||||
C、sinx<
| ||||
D、sinx>
|
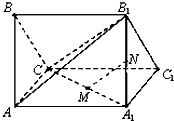 已知三棱柱ABC-A1B1C1,AA1⊥平面ABC,AB=AC=2,∠BAC=90°,四边形AA1C1C为正方形,M,N分别为A1C,A1B1中点.
已知三棱柱ABC-A1B1C1,AA1⊥平面ABC,AB=AC=2,∠BAC=90°,四边形AA1C1C为正方形,M,N分别为A1C,A1B1中点.