题目内容
 已知椭圆C1:
已知椭圆C1:| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
(1)求椭圆的方程;
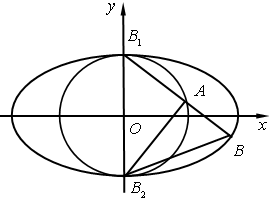
(2)过椭圆短轴的上顶点B1作直线分别与单位圆C2和椭圆C1交于A,B两点(A,B两点均在y轴的右侧),设B2为椭圆的短轴的下顶点,求∠AB2B的最大值.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)利用椭圆C1:
+
=1(a>b>0)的短轴长为单位圆C2:x2+y2=1的直径,且椭圆的离心率为
,求出b,a,即可求椭圆的方程;
(2)设过椭圆的短轴的上顶点B1的直线的方程为y=kx+1,代入C1得B的坐标,确定直线B2A的斜率、直线B2B的斜率的关系,利用向量的数量积公式,求出cos∠AB2B,利用基本不等式,即可求∠AB2B的最大值.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
(2)设过椭圆的短轴的上顶点B1的直线的方程为y=kx+1,代入C1得B的坐标,确定直线B2A的斜率、直线B2B的斜率的关系,利用向量的数量积公式,求出cos∠AB2B,利用基本不等式,即可求∠AB2B的最大值.
解答:
解:(1)由题意知b=1,又e=
=
=
,解得a2=3,
所以椭圆的方程为
+y2=1.…(7分)
(2)由(1)得B1(0,1),B2(0,-1),设过椭圆的短轴的上顶点B1的直线的方程为y=kx+1,
由于B1B2为圆的直径,所以直线B2A的斜率k1=-
.
把y=kx+1代入C1得B(-
,
),
由题意易知k<0,且直线B2B的斜率为k2=
=-
,
所以k1,k2>0,且k1=3k2,…(10分)
又在△B2AB是直角三角形,所以∠AB2B必为锐角.
因为
与
的方向向量分别为(1,k1),(1,k2),
所以
•
=(1,k1)•(1,k2)=1+3
,
又
•
=
•
cos∠AB2B,从而cos∠AB2B=
…(12分)
=
=
≥
,
当且仅当k2=
时,cos∠AB2B取得最小值
,
由∠AB2B为锐角得∠AB2B的最大值为
.…(15分)
| c |
| a |
| ||
| a |
| ||
| 3 |
所以椭圆的方程为
| x2 |
| 3 |
(2)由(1)得B1(0,1),B2(0,-1),设过椭圆的短轴的上顶点B1的直线的方程为y=kx+1,
由于B1B2为圆的直径,所以直线B2A的斜率k1=-
| 1 |
| k |
把y=kx+1代入C1得B(-
| 6k |
| 1+3k2 |
| 1-3k2 |
| 1+3k2 |
由题意易知k<0,且直线B2B的斜率为k2=
| ||
|
| 1 |
| 3k |
所以k1,k2>0,且k1=3k2,…(10分)
又在△B2AB是直角三角形,所以∠AB2B必为锐角.
因为
| B2A |
| B2B |
所以
| B2A |
| B2B |
| k | 2 2 |
又
| B2A |
| B2B |
1+
|
1+
|
1+3
| ||||||||
|
=
1-
|
1-
|
| ||
| 2 |
当且仅当k2=
| ||
| 3 |
| ||
| 2 |
由∠AB2B为锐角得∠AB2B的最大值为
| π |
| 6 |
点评:本题考查椭圆的方程,考查直线与椭圆的位置关系,考查向量的数量积公式,考查基本不等式的运用,考查学生分析解决问题的能力,难度中等.

练习册系列答案
相关题目
某几何体的三视图如图所示,则该几何体的体积是( )
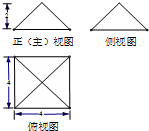

| A、32 | ||||
B、
| ||||
C、
| ||||
D、
|
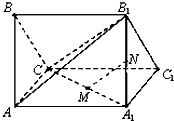 已知三棱柱ABC-A1B1C1,AA1⊥平面ABC,AB=AC=2,∠BAC=90°,四边形AA1C1C为正方形,M,N分别为A1C,A1B1中点.
已知三棱柱ABC-A1B1C1,AA1⊥平面ABC,AB=AC=2,∠BAC=90°,四边形AA1C1C为正方形,M,N分别为A1C,A1B1中点. 如图,已知平面内一动点A到两个定点F1、F2的距离之和为4,线段F1F2的长为2
如图,已知平面内一动点A到两个定点F1、F2的距离之和为4,线段F1F2的长为2 如图,设椭圆
如图,设椭圆