题目内容
如图，如果你在海边沿着海岸线直线前行，请设计一种测量海中两个小岛A，B之间距离的方法．考点：解三角形的实际应用
专题：解三角形
分析：画出图形，利用正弦定理求出D，以及AD的表达式，尽快提供余弦定理求出两个小岛A，B之间距离．
解答：
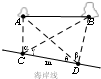解：如图，设C，D是两个观测点，C到D的距离为m，
在C处测出∠ACB=α，∠BCD=γ，
在D处测出∠ADB=β，∠ADC=θ，
据正弦定理，在△BCD中，
=
，
可求得BD=
，（4分）
同理，在△ACD中，可求得AD=
（8分）
在△ADB中，由余弦定理可得：AB=
（10分）
解：如图，设C，D是两个观测点，C到D的距离为m，在C处测出∠ACB=α，∠BCD=γ，
在D处测出∠ADB=β，∠ADC=θ，
据正弦定理，在△BCD中，
| BD |
| sinγ |
| m |
| sin(γ+θ+β) |
可求得BD=
| msinγ |
| sin(γ+θ+β) |
同理，在△ACD中，可求得AD=
| msin(α+γ) |
| sin(α+γ+θ) |
在△ADB中，由余弦定理可得：AB=
| AD2+BD2-2AD•BDcosβ |
点评：本题考查正弦定理以及余弦定理的应用，基本知识的考查．
练习册系列答案
学而优暑期衔接南京大学出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
如图，已知平面内一动点A到两个定点F1、F2的距离之和为4，线段F1F2的长为2
如图，设椭圆