题目内容
某市组织一次高三调研考试,考试后统计的数学成绩服从正态分布,其密度函数f(x)=
e-
(x∈(-∞,+∞)),则下列命题不正确的是( )
| 1 | ||
|
| (x-90)2 |
| 400 |
| A、该市这次考试的数学平均成绩为90分 |
| B、分数在120分以上的人数与分数在60分以下的人数相同 |
| C、分数在110分以上的人数与分数在50分以下的人数相同 |
| D、该市这次考试的数学标准差为20 |
考点:正态分布曲线的特点及曲线所表示的意义
专题:概率与统计
分析:根据数学成绩符合正态分布和所给的函数式,得到这组数据的均值和标准差,判断出A,D选项的正误,根据数据的对称性判断出B,C选项的正误.
解答:
解:∵数学成绩服从正态分布,
其密度函数为f(x)=
e-
(x∈R),
∴μ=90,σ=20,
∴这次考试的数学平均成绩是90,故A正确,
这次考试的数学标准差是20,故D正确,
∵正态曲线关于x=90对称,
∴在110分以上的人数和50分以下的人数相同,故C不正确,
分数在120以上的和分数在60分以下的相同,故D正确,
故选:C.
其密度函数为f(x)=
| 1 | ||
|
| (x-90)2 |
| 400 |
∴μ=90,σ=20,
∴这次考试的数学平均成绩是90,故A正确,
这次考试的数学标准差是20,故D正确,
∵正态曲线关于x=90对称,
∴在110分以上的人数和50分以下的人数相同,故C不正确,
分数在120以上的和分数在60分以下的相同,故D正确,
故选:C.
点评:本题考查正态分布曲线的特点及其曲线所表示的意义,考查曲线的对称性,考查密度函数的结构,本题是一个基础题.

练习册系列答案
相关题目
某几何体的三视图如图所示,则该几何体的体积是( )
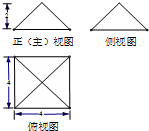

| A、32 | ||||
B、
| ||||
C、
| ||||
D、
|
要得到函数y=cos(2x+
)的图象,只需将y=cos2x的图象( )
| π |
| 4 |
A、向右平移
| ||
B、向左平移
| ||
C、向左平移
| ||
D、向右平移
|
下面是关于f(x)=xsin(
-x)的四个命题:
p1:图象关于原点对称
p2:图象关于y轴对称
p3:在[-3π,3π]上有6个零点
p4:在[-3π,3π]上有7个零点,
其中的正确的为( )
| π |
| 2 |
p1:图象关于原点对称
p2:图象关于y轴对称
p3:在[-3π,3π]上有6个零点
p4:在[-3π,3π]上有7个零点,
其中的正确的为( )
| A、p1,p3 |
| B、p2,p3 |
| C、p1,p4 |
| D、p2,p4 |
下列不等式成立的是( )
| A、ex<x+1 | ||||
| B、lnx>x-1 | ||||
C、sinx<
| ||||
D、sinx>
|
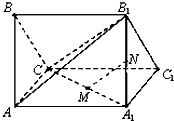 已知三棱柱ABC-A1B1C1,AA1⊥平面ABC,AB=AC=2,∠BAC=90°,四边形AA1C1C为正方形,M,N分别为A1C,A1B1中点.
已知三棱柱ABC-A1B1C1,AA1⊥平面ABC,AB=AC=2,∠BAC=90°,四边形AA1C1C为正方形,M,N分别为A1C,A1B1中点. 如图,设椭圆
如图,设椭圆