题目内容
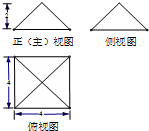
某四棱锥的三视图如图所示,该四棱锥的体积为( )


| A、8 | B、16 | C、24 | D、32 |
考点:由三视图求面积、体积
专题:计算题,空间位置关系与距离
分析:根据三视图可得四棱锥的一条侧棱与底面垂直,底面为直角梯形,判断三视图的数据所对应的几何量,把数据代入棱锥的体积公式计算可得答案.
解答:
解:由三视图知:几何体为如图放置的四棱锥,四棱锥的一条棱SA与底面ABCD垂直,高为4,
四棱锥的底面为直角梯形,且直角梯形的两底边长分别为2,4,高为4,
∴四棱锥的体积V=
×
×4×4=16.
故选:B.

四棱锥的底面为直角梯形,且直角梯形的两底边长分别为2,4,高为4,
∴四棱锥的体积V=
| 1 |
| 3 |
| 2+4 |
| 2 |
故选:B.

点评:本题考查了由三视图求四棱锥的体积,根据三视图判断数据所对应的几何量是解答本题的关键.

练习册系列答案
相关题目
已知f(x)=f′(1)x2,则f′(0)等于( )
| A、0 | B、1 | C、2 | D、3 |
数列{an}的通项an=
,则数列{an}中的最大值是( )
| n |
| n2+90 |
A、3
| ||||
| B、19 | ||||
C、
| ||||
D、
|
| ∫ | 0 -2 |
| 4-x2 |
| A、4π | ||
| B、2π | ||
| C、π | ||
D、
|
方程
=
表示的曲线为( )
| (x-2)2+(y-2)2 |
| |3x-4y-6| |
| 5 |
| A、抛物线 | B、椭圆 | C、双曲线 | D、圆 |
某几何体的三视图如图所示,则该几何体的体积是( )

| A、32 | ||||
B、
| ||||
C、
| ||||
D、
|