题目内容
7.已知F是双曲线C:x2-$\frac{{y}^{2}}{8}$=1的右焦点,若P是C的左支上一点,A(0,6$\sqrt{6}$)是y轴上一点,则△APF面积的最小值为6+9$\sqrt{6}$.分析 求得双曲线的焦点,直线AF的方程以及AF的长,设直线y=-2$\sqrt{6}$x+t与双曲线相切,且切点为左支上一点,联立双曲线方程,消去y,由判别式为0,求得m,再由平行直线的距离公式可得三角形的面积的最小值.
解答 解:双曲线C:x2-$\frac{{y}^{2}}{8}$=1的右焦点为(3,0),
由A(0,6$\sqrt{6}$),可得直线AF的方程为y=-2$\sqrt{6}$x+6$\sqrt{6}$,
|AF|=$\sqrt{9+(6\sqrt{6})^{2}}$=15,
设直线y=-2$\sqrt{6}$x+t与双曲线相切,且切点为左支上一点,
联立$\left\{\begin{array}{l}{y=t-2\sqrt{6}x}\\{8{x}^{2}-{y}^{2}=8}\end{array}\right.$,可得16x2-4$\sqrt{6}$tx+t2+8=0,
由判别式为0,即有96t2-4×16(t2+8)=0,
解得t=-4(4舍去),
可得P到直线AF的距离为d=$\frac{|6\sqrt{6}+4|}{\sqrt{1+24}}$=$\frac{4+6\sqrt{6}}{5}$,
即有△APF的面积的最小值为$\frac{1}{2}$d•|AF|=$\frac{1}{2}$×$\frac{4+6\sqrt{6}}{5}$×15=6+9$\sqrt{6}$.
故答案为:6+9$\sqrt{6}$.
点评 本题考查三角形的面积的最小值的求法,注意运用联立直线方程和双曲线方程,运用判别式为0,考查化简整理的运算能力,属于中档题.

练习册系列答案
相关题目
17.已知A,B分别是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右顶点,P是双曲线C右支上位于第一象限的动点,设PA,PB的斜率分别为k1,k2,则k1+k2的取值范围为( )
| A. | ($\frac{2b}{a}$,+∞) | B. | ($\frac{b}{a}$,+∞) | C. | [$\frac{b}{a}$,+∞) | D. | [$\frac{b}{a}$,$\frac{2b}{a}$) |
18.数列{an}满足a1=1,且an+1=a1+an+n(n∈N*),则$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+…+$\frac{1}{{a}_{2016}}$等于( )
| A. | $\frac{2015}{2016}$ | B. | $\frac{4028}{2015}$ | C. | $\frac{4032}{2017}$ | D. | $\frac{2014}{2015}$ |
19.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1,F2,c是半焦轴距,P是双曲线上异于顶点的点,满足ctan∠PF1F2=atan∠PF2F1,则双曲线的离心率e的取值范围是( )
| A. | (1,1+$\sqrt{2}$) | B. | ($\sqrt{2}$,1+$\sqrt{2}$) | C. | (1+$\sqrt{2}$,1+$\sqrt{3}$) | D. | (1+$\sqrt{2}$,+∞) |
17.已知点F1是抛物线C:x2=4y的焦点,点F2为抛物线C的对称轴与其准线的交点,过F2作抛物线C的切线,切点为A,若点A恰好在以F1,F2为焦点的双曲线上,则双曲线的离心率为( )
| A. | $\frac{\sqrt{6}-\sqrt{2}}{2}$ | B. | $\sqrt{2}$-1 | C. | $\sqrt{2}$+1 | D. | $\frac{\sqrt{6}+\sqrt{2}}{2}$ |
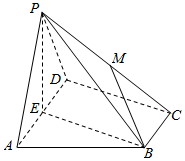 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,E为AD的中点,M是棱PC的中点,PA=PD=2,$BC=\frac{1}{2}AD=1$,$CD=\sqrt{3}$.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,E为AD的中点,M是棱PC的中点,PA=PD=2,$BC=\frac{1}{2}AD=1$,$CD=\sqrt{3}$.