题目内容
12.已知直线y=2x是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的一条渐近线,点A(1,0),M(m,n)(n≠0)都在双曲线C上,直线AM与y轴相交于点P,设坐标原点为O.(1)求双曲线C的方程,并求出点P的坐标(用m,n表示);
(2)设点M关于y轴的对称点为N,直线AN与y轴相交于点Q,问:在x轴上是否存在定点T,使得TP⊥TQ?若存在,求出点T的坐标;若不存在,请说明理由.
(3)若过点D(0,2)的直线l与双曲线C交于R,S两点,且|$\overrightarrow{OR}$+$\overrightarrow{OS}$|=|$\overrightarrow{RS}$|,试求直线l的方程.
分析 (1)求得双曲线的渐近线方程,可得b=2a,由题意可得a=1,b=2,可得双曲线的方程,求出直线AM的方程,可令x=0,求得P的坐标;
(2)求得对称点N的坐标,直线AN方程,令x=0,可得N的坐标,假设存在T,运用两直线垂直的条件:斜率之积为-1,结合M在双曲线上,化简整理,即可得到定点T;
(3)设出直线l的方程,代入双曲线的方程,运用韦达定理,由向量数量积的性质,可得向量OR,OS的数量积为0,化简整理,解方程可得k的值,检验判别式大于0成立,进而得到直线l的方程.
解答 解:(1)双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的渐近线为y=±$\frac{b}{a}$x,
由题意可得$\frac{b}{a}$=2,a=1,可得b=2,
即有双曲线的方程为x2-$\frac{{y}^{2}}{4}$=1,
又AM的方程为y=$\frac{n}{m-1}$(x-1),
令x=0,可得P(0,$\frac{n}{1-m}$);
(2)点M关于y轴的对称点为N(-m,n),
直线AN的方程为y=$\frac{n}{-m-1}$(x-1),
令x=0,可得Q(0,$\frac{n}{1+m}$),
假设x轴存在点T(t,0),使得TP⊥TQ.
即有kTP•kTQ=-1,
即为$\frac{\frac{n}{1-m}}{-t}$•$\frac{\frac{n}{1+m}}{-t}$=-1,
可得t2=$\frac{{n}^{2}}{{m}^{2}-1}$,
由(m,n)满足双曲线的方程,可得m2-$\frac{{n}^{2}}{4}$=1,
即有$\frac{{n}^{2}}{{m}^{2}-1}$=4,
可得t2=4,解得t=±2,
故存在点T(±2,0),使得TP⊥TQ;
(3)可设过点D(0,2)的直线l:y=kx+2,
代入双曲线的方程可得(4-k2)x2-4kx-8=0,
即有△=16k2+32(4-k2)>0,即k2<8,
设R(x1,y1),S(x2,y2),
可得x1+x2=$\frac{4k}{4-{k}^{2}}$,x1x2=-$\frac{8}{4-{k}^{2}}$,
由|$\overrightarrow{OR}$+$\overrightarrow{OS}$|=|$\overrightarrow{RS}$|=|$\overrightarrow{OS}$-$\overrightarrow{OR}$|,
两边平方可得$\overrightarrow{OS}$•$\overrightarrow{OR}$=0,
即有x1x2+y1y2=0,
即x1x2+(kx1+2)(kx2+2)=(1+k2)x1x2+2k(x1+x2)+4=0,
即为(1+k2)•(-$\frac{8}{4-{k}^{2}}$)+2k($\frac{4k}{4-{k}^{2}}$)+4=0,
化简可得k2=2,检验判别式大于0成立,
即有k=±$\sqrt{2}$,
则所求直线的方程为y=±$\sqrt{2}$x+2.
点评 本题考查双曲线的方程和性质,考查对称思想的运用,以及两直线垂直的条件,联立直线方程和双曲线方程,运用韦达定理和向量垂直的条件:数量积为0,考查化简整理的运算能力,属于中档题.

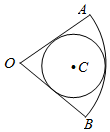 如图,圆C内切于扇形AOB,$∠AOB=\frac{π}{3}$,若向扇形AOB内随机投掷600个点,则落入圆内的点的个数估计值为( )
如图,圆C内切于扇形AOB,$∠AOB=\frac{π}{3}$,若向扇形AOB内随机投掷600个点,则落入圆内的点的个数估计值为( )| A. | 100 | B. | 200 | C. | 400 | D. | 450 |
| A. | $\frac{3+\sqrt{7}}{2}$ | B. | $\frac{3-\sqrt{7}}{2}$ | C. | 3-$\sqrt{7}$ | D. | 3+$\sqrt{7}$ |
| A. | $-\frac{20}{11}$ | B. | $\frac{20}{11}$ | C. | $-\frac{9}{5}$ | D. | $\frac{9}{5}$ |
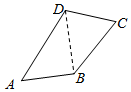 如图,已知四边形ABCD中,AB=CD=1,AD=$\sqrt{2}$BC=2,∠A+∠C=$\frac{3π}{4}$.则BD的长为$\frac{\sqrt{65}}{5}$.
如图,已知四边形ABCD中,AB=CD=1,AD=$\sqrt{2}$BC=2,∠A+∠C=$\frac{3π}{4}$.则BD的长为$\frac{\sqrt{65}}{5}$.