题目内容
17.已知A,B分别是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右顶点,P是双曲线C右支上位于第一象限的动点,设PA,PB的斜率分别为k1,k2,则k1+k2的取值范围为( )| A. | ($\frac{2b}{a}$,+∞) | B. | ($\frac{b}{a}$,+∞) | C. | [$\frac{b}{a}$,+∞) | D. | [$\frac{b}{a}$,$\frac{2b}{a}$) |
分析 由题意可得A(-a,0),B(a,0),设P(m,n),代入双曲线的方程,运用直线的斜率公式可得k1k2=$\frac{{b}^{2}}{{a}^{2}}$,k1,k2>0,再由基本不等式即可得到k1+k2的取值范围.
解答 解:由题意可得A(-a,0),B(a,0),设P(m,n),
可得$\frac{{m}^{2}}{{a}^{2}}$-$\frac{{n}^{2}}{{b}^{2}}$=1,即有$\frac{{n}^{2}}{{m}^{2}-{a}^{2}}$=$\frac{{b}^{2}}{{a}^{2}}$,
可得k1k2=$\frac{n}{m+a}$•$\frac{n}{m-a}$=$\frac{{n}^{2}}{{m}^{2}-{a}^{2}}$=$\frac{{b}^{2}}{{a}^{2}}$,k1,k2>0,
则k1+k2≥2$\sqrt{{k}_{1}{k}_{2}}$=$\frac{2b}{a}$,
由A,B为左右顶点,可得k1≠k2,
则k1+k2>$\frac{2b}{a}$,
故选:A.
点评 本题考查双曲线的方程和性质,注意运用点满足双曲线的方程,以及直线的斜率公式,考查基本不等式的运用以及运算能力,属于中档题.

练习册系列答案
相关题目
18.对满足条件x≥0,y≥0,x+y≤2的实数x,y,记z=|x-1|+|y-1|,则z的最大值为( )
| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
5.已知A为△ABC的一个内角,且$sinA+cosA=\frac{{\sqrt{2}}}{3}$,则△ABC的形状是( )
| A. | 锐角三角形 | B. | 钝角三角形 | C. | 直角三角形 | D. | 不确定 |
2.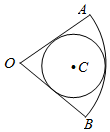 如图,圆C内切于扇形AOB,$∠AOB=\frac{π}{3}$,若向扇形AOB内随机投掷600个点,则落入圆内的点的个数估计值为( )
如图,圆C内切于扇形AOB,$∠AOB=\frac{π}{3}$,若向扇形AOB内随机投掷600个点,则落入圆内的点的个数估计值为( )
 如图,圆C内切于扇形AOB,$∠AOB=\frac{π}{3}$,若向扇形AOB内随机投掷600个点,则落入圆内的点的个数估计值为( )
如图,圆C内切于扇形AOB,$∠AOB=\frac{π}{3}$,若向扇形AOB内随机投掷600个点,则落入圆内的点的个数估计值为( )| A. | 100 | B. | 200 | C. | 400 | D. | 450 |
9.已知双曲线$\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{{b}^{2}}$=1(a>0,b>0)与圆x2+y2=c2(c=$\sqrt{{a}^{2}+{b}^{2}}$)交A、B、C、D四点,若四边形ABCD是正方形,则双曲线的渐近线方程为( )
| A. | y=±$\sqrt{1+\sqrt{2}}$x | B. | y=±$\sqrt{2}$x | C. | y=±$\frac{\sqrt{2}}{2}$x | D. | y=±$\sqrt{\sqrt{2}-1}$x |