题目内容
15.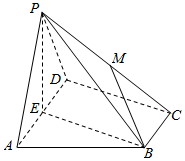 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,E为AD的中点,M是棱PC的中点,PA=PD=2,$BC=\frac{1}{2}AD=1$,$CD=\sqrt{3}$.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,E为AD的中点,M是棱PC的中点,PA=PD=2,$BC=\frac{1}{2}AD=1$,$CD=\sqrt{3}$.(1)求证:PE⊥平面ABCD;
(2)求直线BM与平面ABCD所成角的正切值;
(3)求直线BM与CD所成角的余弦值.
分析 (1)推导出PE⊥AD,平面PAD⊥平面ABCD,由此能证明PE⊥平面ABCD.
(2)连结EC,取EC中点H,连结MH、HB,则MH∥PE,从而∠MBH即为BM与平面ABCD所成角,由此能求出直线BM与平面ABCD所成角的正切值.
(3)由CD∥BE,得直线BM与CD所成角即为直线BM与BE所成角,由此能求出直线BM与CD所成角的余弦值.
解答 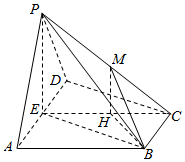 证明:(1)∵PA=PD,E为AD的中点,∴PE⊥AD
证明:(1)∵PA=PD,E为AD的中点,∴PE⊥AD
又∵平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,
∴PE⊥平面ABCD.
解:(2)连结EC,取EC中点H,连结MH、HB,
∵M是PC的中点,H是EC的中点,∴MH∥PE,
由(1)知PE⊥平面ABCD,∴MH⊥平面ABCD,
∴HB是BM在平面ABCD内的射影,
∴∠MBH即为BM与平面ABCD所成角,
∵AD∥BC,BC=$\frac{1}{2}$AD,E为AD的中点,∠ADC=90°,
∴四边形BCDE为矩形,∴EC=2,HB=$\frac{1}{2}EC=1$,
又∵MH=$\frac{1}{2}$PE=$\frac{\sqrt{3}}{2}$,∴△MHB中,tan$∠MBH=\frac{MH}{HB}$=$\frac{\sqrt{3}}{2}$,
∴直线BM与平面ABCD所成角的正切值为$\frac{\sqrt{3}}{2}$.
(3)由(2)知CD∥BE,
∴直线BM与CD所成角即为直线BM与BE所成角
连接ME,Rt△MHE中,$ME=\frac{{\sqrt{7}}}{2}$,
Rt△MHB中,$BM=\frac{{\sqrt{7}}}{2}$,又$BE=CD=\sqrt{3}$,
∴△MEB中,$cos∠MBE=\frac{{B{M^2}+B{E^2}-M{E^2}}}{2BM•BE}=\frac{{\frac{7}{4}+3-\frac{7}{4}}}{{2×\frac{{\sqrt{7}}}{2}×\sqrt{3}}}=\frac{{\sqrt{21}}}{7}$,
∴直线BM与CD所成角的余弦值为$\frac{{\sqrt{21}}}{7}$.
点评 本题考查线面垂直的证明,考查线面角的正弦值和线线角的余弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

| A. | 锐角三角形 | B. | 钝角三角形 | C. | 直角三角形 | D. | 不确定 |
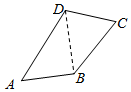 如图,已知四边形ABCD中,AB=CD=1,AD=$\sqrt{2}$BC=2,∠A+∠C=$\frac{3π}{4}$.则BD的长为$\frac{\sqrt{65}}{5}$.
如图,已知四边形ABCD中,AB=CD=1,AD=$\sqrt{2}$BC=2,∠A+∠C=$\frac{3π}{4}$.则BD的长为$\frac{\sqrt{65}}{5}$.