题目内容
18.数列{an}满足a1=1,且an+1=a1+an+n(n∈N*),则$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+…+$\frac{1}{{a}_{2016}}$等于( )| A. | $\frac{2015}{2016}$ | B. | $\frac{4028}{2015}$ | C. | $\frac{4032}{2017}$ | D. | $\frac{2014}{2015}$ |
分析 a1=1,an+1=a1+an+n(n∈N*),写出an+1-an=n+1,采用累加法,求得an=$\frac{n(n+1)}{2}$,$\frac{1}{{a}_{n}}=\frac{2}{n(n+1)}$=2($\frac{1}{n}-\frac{1}{n+1}$),
$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+…+$\frac{1}{{a}_{2016}}$=2(1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$…+$\frac{1}{2016}$-$\frac{1}{2017}$)=$\frac{4032}{2017}$.
解答 解:a1=1,an+1=a1+an+n(n∈N*),
∴an+1-an=n+1,
a2-a1=2,
a3-a2=3,
…an-an-1=n,
累加得:an-a1=2+3+4+…+n,
∴an=1+2+3+…+n=$\frac{n(n+1)}{2}$,
$\frac{1}{{a}_{n}}=\frac{2}{n(n+1)}$=2($\frac{1}{n}-\frac{1}{n+1}$),
∴$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+…+$\frac{1}{{a}_{2016}}$=2(1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$…+$\frac{1}{2016}$-$\frac{1}{2017}$),
=2(1-$\frac{1}{2017}$),
=$\frac{4032}{2017}$,
故答案选:C.
点评 本题考查采用累加法求数列的通项公式,裂项法求前n项和,属于中档题.

练习册系列答案
相关题目
18.对满足条件x≥0,y≥0,x+y≤2的实数x,y,记z=|x-1|+|y-1|,则z的最大值为( )
| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
9.已知双曲线$\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{{b}^{2}}$=1(a>0,b>0)与圆x2+y2=c2(c=$\sqrt{{a}^{2}+{b}^{2}}$)交A、B、C、D四点,若四边形ABCD是正方形,则双曲线的渐近线方程为( )
| A. | y=±$\sqrt{1+\sqrt{2}}$x | B. | y=±$\sqrt{2}$x | C. | y=±$\frac{\sqrt{2}}{2}$x | D. | y=±$\sqrt{\sqrt{2}-1}$x |
13.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{3}$=1的一个焦点在抛物线y2=8x的准线上,则该双曲线的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | 2 |
7.已知F是双曲线C:x2-$\frac{{y}^{2}}{8}$=1的右焦点,若P是C的左支上一点,A(0,6$\sqrt{6}$)是y轴上一点,则△APF面积的最小值为6+9$\sqrt{6}$.
8.以双曲线$\frac{{x}^{2}}{3}$-y2=1的左右焦点为焦点,离心率为$\frac{1}{2}$的椭圆的标准方程为( )
| A. | $\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{16}$=1 | B. | $\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{8}$=1 | C. | $\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{12}$=1 | D. | $\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{12}$=1 |
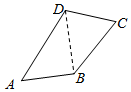 如图,已知四边形ABCD中,AB=CD=1,AD=$\sqrt{2}$BC=2,∠A+∠C=$\frac{3π}{4}$.则BD的长为$\frac{\sqrt{65}}{5}$.
如图,已知四边形ABCD中,AB=CD=1,AD=$\sqrt{2}$BC=2,∠A+∠C=$\frac{3π}{4}$.则BD的长为$\frac{\sqrt{65}}{5}$.