题目内容
17.已知点F1是抛物线C:x2=4y的焦点,点F2为抛物线C的对称轴与其准线的交点,过F2作抛物线C的切线,切点为A,若点A恰好在以F1,F2为焦点的双曲线上,则双曲线的离心率为( )| A. | $\frac{\sqrt{6}-\sqrt{2}}{2}$ | B. | $\sqrt{2}$-1 | C. | $\sqrt{2}$+1 | D. | $\frac{\sqrt{6}+\sqrt{2}}{2}$ |
分析 利用直线F2A与抛物线相切,求出A的坐标,利用双曲线的定义,即可求得双曲线的离心率.
解答 解:设直线F2A的方程为y=kx-1,代入x2=4y,可得x2=4(kx-1),
即x2-4kx+4=0,
∴△=16k2-16=0,∴k=±1,
∴A(2,1),
∴双曲线的实轴长为AF2-AF1=2($\sqrt{2}$-1),
∴双曲线的离心率为$\frac{2}{2(\sqrt{2}-1)}$=$\sqrt{2}$+1.
故选:C.
点评 本题考查抛物线的性质,考查双曲线、抛物线的定义,考查学生分析解决问题的能力,解答此题的关键是求出A的坐标,属中档题.

练习册系列答案
相关题目
7.已知F是双曲线C:x2-$\frac{{y}^{2}}{8}$=1的右焦点,若P是C的左支上一点,A(0,6$\sqrt{6}$)是y轴上一点,则△APF面积的最小值为6+9$\sqrt{6}$.
8.以双曲线$\frac{{x}^{2}}{3}$-y2=1的左右焦点为焦点,离心率为$\frac{1}{2}$的椭圆的标准方程为( )
| A. | $\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{16}$=1 | B. | $\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{8}$=1 | C. | $\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{12}$=1 | D. | $\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{12}$=1 |
12.已知实数x,y满足条件$\left\{\begin{array}{l}y≤x\\ x+y≥2\\ 2x+y≥6\end{array}\right.$,则z=3x+2y的取值范围是( )
| A. | (-∞,10] | B. | [5,10] | C. | [8,+∞) | D. | [8,10] |
9.阅读如图的程序框图,运行相应的程序,输出的结果为( )
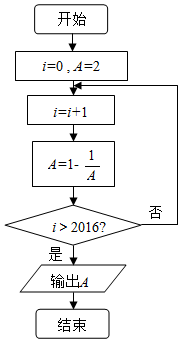

| A. | -2 | B. | $\frac{1}{2}$ | C. | -1 | D. | 2 |
6.“a≠1”是“a2≠1”的( )
| A. | 充分不必条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |