题目内容
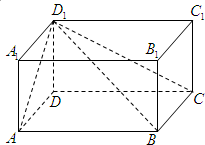如图，长方体ABCD-A1B1C1D1中，AA1=1，D1C与面ABCD所成的角为30°，D1A与BC所成的角为45°，则D1B与面BCC1B1所成角的正弦值为考点：直线与平面所成的角
专题：计算题,空间角
分析：长方体ABCD-A1B1C1D1中，先计算出BD1=
，D1C1=
，再由直线BD1与平面BCC1B1所成角为∠D1BC1，由此能求出直线BD1与平面BCC1B1所成角的正弦值．
| 5 |
| 3 |
解答：
解：∵长方体ABCD-A1B1C1D1中，AA1=1，D1C与面ABCD所成的角为30°，D1A与BC所成的角为45°，
∴DC=
，AD=1
∴BD1=
，D1C1=
，
∵直线BD1与平面BCC1B1所成角为∠D1BC1，
∴直线BD1与平面BCC1B1所成角的正弦值sin∠D1BC1=
=
=
．
故答案为：
．
∴DC=
| 3 |
∴BD1=
| 5 |
| 3 |
∵直线BD1与平面BCC1B1所成角为∠D1BC1，
∴直线BD1与平面BCC1B1所成角的正弦值sin∠D1BC1=
| D1C1 |
| BD1 |
| ||
|
| ||
| 5 |
故答案为：
| ||
| 5 |
点评：本题考查直线与平面所成角的正弦值的求法，解题时要认真审题，注意等价转化思想的合理运用．
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
相关题目