题目内容
函数y=2sin2x+3cos2x-4的最小正周期为 .
考点:三角函数的周期性及其求法
专题:三角函数的图像与性质
分析:将函数进行化简,利用三角函数的周期公式即可得到结论.
解答:
解:∵y=2sin2x+3cos2x-4
=y=2+cos2x-4
=
+
cos2x-2
=
cos2x-
,
∴三角函数的周期T=
=π,
故答案为:π
=y=2+cos2x-4
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 3 |
| 2 |
∴三角函数的周期T=
| 2π |
| 2 |
故答案为:π
点评:本题主要考查三角函数周期的计算,将三角函数进行化简是解决本题的关键,比较基础.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
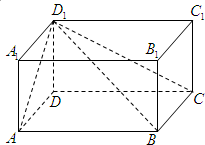 如图,长方体ABCD-A1B1C1D1中,AA1=1,D1C与面ABCD所成的角为30°,D1A与BC所成的角为45°,则D1B与面BCC1B1所成角的正弦值为
如图,长方体ABCD-A1B1C1D1中,AA1=1,D1C与面ABCD所成的角为30°,D1A与BC所成的角为45°,则D1B与面BCC1B1所成角的正弦值为