题目内容
关于x的不等式
>0,x的取值范围是 .
| |x|-x |
考点:其他不等式的解法
专题:不等式的解法及应用
分析:根据根式成立的条件,建立不等式关系即可得到结论.
解答:
解:∵
>0,
∴|x|-x>0,
即|x|>x,
∴x<0,
即x的取值范围是(-∞,0),
故答案为:(-∞,0)
| |x|-x |
∴|x|-x>0,
即|x|>x,
∴x<0,
即x的取值范围是(-∞,0),
故答案为:(-∞,0)
点评:本题主要考查不等式的解法,利用绝对值的意义是解决本题的关键,比较基础.

练习册系列答案
相关题目
设sin(θ+
)=
,则sin2θ=( )
| π |
| 4 |
| 1 |
| 4 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
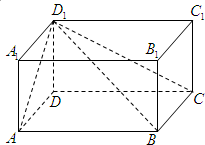 如图,长方体ABCD-A1B1C1D1中,AA1=1,D1C与面ABCD所成的角为30°,D1A与BC所成的角为45°,则D1B与面BCC1B1所成角的正弦值为
如图,长方体ABCD-A1B1C1D1中,AA1=1,D1C与面ABCD所成的角为30°,D1A与BC所成的角为45°,则D1B与面BCC1B1所成角的正弦值为