题目内容
设函数f(x)的导数为f′(x),且f(x)=f′(
)sinx+cosx,则f′(
)= .
| π |
| 2 |
| π |
| 4 |
考点:导数的运算
专题:导数的综合应用
分析:对f(x)=f′(
)sinx+cosx两边求导,令x=
可得f′(
),再令x=
即可求得f′(
).
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
解答:
解:由f(x)=f′(
)sinx+cosx,得f′(x)=f′(
)cosx-sinx,
则f′(
)=f′(
)•cos
-sin
,解得f′(
)=-1,
∴f′(
)=-cosx-sinx=-cos
-sin
=-
-
=-
,
故答案为:-
.
| π |
| 2 |
| π |
| 2 |
则f′(
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
∴f′(
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| ||
| 2 |
| ||
| 2 |
| 2 |
故答案为:-
| 2 |
点评:本题考查导数的运算、三角函数值,考查学生对问题的分析解决能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
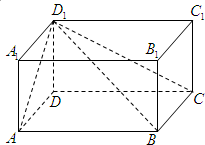 如图,长方体ABCD-A1B1C1D1中,AA1=1,D1C与面ABCD所成的角为30°,D1A与BC所成的角为45°,则D1B与面BCC1B1所成角的正弦值为
如图,长方体ABCD-A1B1C1D1中,AA1=1,D1C与面ABCD所成的角为30°,D1A与BC所成的角为45°,则D1B与面BCC1B1所成角的正弦值为