题目内容
若不等式ax2+bx-2<0的解集为{x|-2<x<
},则a+b等于 .
| 1 |
| 4 |
考点:一元二次不等式的解法
专题:不等式的解法及应用
分析:根据不等式的解集合对应方程之间的关系即可得到结论.
解答:
解:∵不等式ax2+bx-2<0的解集为{x|-2<x<
},
∴-2,
是对应方程ax2+bx-2=0的两个根,且a>0,
∴
,
解得a=4,b=7,
∴a+b=4+7=11,
故答案为:11
| 1 |
| 4 |
∴-2,
| 1 |
| 4 |
∴
|
解得a=4,b=7,
∴a+b=4+7=11,
故答案为:11
点评:本题主要考查一元二次不等式的应用,根据一元二次不等式和二次方程之间的关系,转化为根与系数之间的关系是解决本题的关键.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
设全集U=R,集合A={x∈R|x2-2x<0},B={y|y=ex+1,x∈R},则A∩B=( )
| A、{x|1≤x<2} |
| B、{x|x>2} |
| C、{x|x>1} |
| D、{x|1<x<2} |
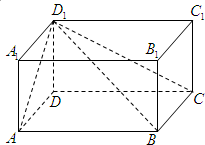 如图,长方体ABCD-A1B1C1D1中,AA1=1,D1C与面ABCD所成的角为30°,D1A与BC所成的角为45°,则D1B与面BCC1B1所成角的正弦值为
如图,长方体ABCD-A1B1C1D1中,AA1=1,D1C与面ABCD所成的角为30°,D1A与BC所成的角为45°,则D1B与面BCC1B1所成角的正弦值为