题目内容
函数f(x)=sin2x+cosx,x∈R的最大值等于 .
考点:同角三角函数基本关系的运用,三角函数的最值
专题:计算题,三角函数的求值
分析:先利用同角三角函数基本关系,再利用配方法,即可求出函数的最大值.
解答:
解:∵f(x)=sin2x+cosx=1-cos2x+cosx=-(cosx-
)2+
,
∴当cosx=
时,函数f(x)=sin2x+cosx,x∈R取得最大值
,
故答案为:
.
| 1 |
| 2 |
| 5 |
| 4 |
∴当cosx=
| 1 |
| 2 |
| 5 |
| 4 |
故答案为:
| 5 |
| 4 |
点评:本题考查同角三角函数基本关系的运用,考查配方法的运用,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
设全集U=R,集合A={x∈R|x2-2x<0},B={y|y=ex+1,x∈R},则A∩B=( )
| A、{x|1≤x<2} |
| B、{x|x>2} |
| C、{x|x>1} |
| D、{x|1<x<2} |
设sin(θ+
)=
,则sin2θ=( )
| π |
| 4 |
| 1 |
| 4 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
已知条件p:x<1,条件q:
>1,则p是q成立的( )
| 1 |
| x |
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
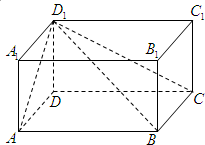 如图,长方体ABCD-A1B1C1D1中,AA1=1,D1C与面ABCD所成的角为30°,D1A与BC所成的角为45°,则D1B与面BCC1B1所成角的正弦值为
如图,长方体ABCD-A1B1C1D1中,AA1=1,D1C与面ABCD所成的角为30°,D1A与BC所成的角为45°,则D1B与面BCC1B1所成角的正弦值为