题目内容
过点A(1,2)的直线与⊙O:(x-3)2+(y+1)2=25相交,所得最短的弦的长 .
考点:直线与圆相交的性质
专题:计算题,直线与圆
分析:由题意,弦长最短时,OA与直线垂直,利用勾股定理,即可得出结论.
解答:
解:由题意,弦长最短时,OA与直线垂直.
∵A(1,2),O(3,-1),
∴OA=
=
,
∴所得最短的弦的长2
=4
,
故答案为:4
.
∵A(1,2),O(3,-1),
∴OA=
| (3-1)2+(-1-2)2 |
| 13 |
∴所得最短的弦的长2
| 25-13 |
| 3 |
故答案为:4
| 3 |
点评:本题考查直线和圆相交的性质,点到直线的距离公式,弦长公式的应用,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
函数f(x)=3x-6的零点是( )
| A、0 | B、3 | C、2 | D、-6 |
下列各式错误的是( )
| A、30.8>30.7 | ||||
| B、0.75-0.1<0.750.1 | ||||
C、(
| ||||
| D、0.50.4>0.50.6 |
已知三角形ABC的三边长a,b,c成等差数列,且a2+b2+c2=84,则实数b的取值范围
是( )
是( )
A、(0,2
| ||||
B、(2
| ||||
C、(0,2
| ||||
D、[2
|
已知集合M={2,4,6,8},N={1,2},P={x|x=
,a∈M,b∈N},则集合P的真子集的个数为( )
| a |
| b |
| A、4 | B、6 | C、15 | D、63 |
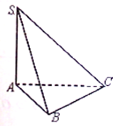 如图,在三棱锥S-ABC中,SA⊥平面ABC,AB=2,BC=3,AB⊥BC,二面角S-BC-A为
如图,在三棱锥S-ABC中,SA⊥平面ABC,AB=2,BC=3,AB⊥BC,二面角S-BC-A为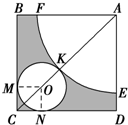 如图所示,在边长为5+
如图所示,在边长为5+