题目内容
4.若直线y=k(x+3)与圆x2+y2-2x=3相切,则k=±$\frac{\sqrt{3}}{3}$.分析 求出圆x2+y2-2x=3的圆心,半径,由直线y=k(x+3)与圆x2+y2-2x=3相切,知圆心(1,0)到直线y=k(x+3)的距离等于圆半径,由此能求出k.
解答 解:圆x2+y2-2x=3的圆心为(1,0),
半径r=$\frac{1}{2}\sqrt{4+12}$=2,
∵直线y=k(x+3)与圆x2+y2-2x=3相切,
∴圆心(1,0)到直线y=k(x+3)的距离:
d=$\frac{|k+3k|}{\sqrt{{k}^{2}+1}}$=2,
解得k=±$\frac{\sqrt{3}}{3}$.
故答案为:$±\frac{{\sqrt{3}}}{3}$.
点评 本题考查直线的斜率的求法,考查圆的性质、直线与圆的位置关系,考查推理论证能力、运算求解能力,考查转化化归思想、数形结合思想,是中档题.

练习册系列答案
相关题目
14.已知$sinα-2cosα=\frac{{\sqrt{10}}}{2}$,则tan2α=( )
| A. | $\frac{4}{3}$ | B. | $-\frac{3}{4}$ | C. | $\frac{3}{4}$ | D. | $-\frac{4}{3}$ |
15.下列命题中错误的是( )
| A. | 如果平面α⊥平面γ,平面β⊥平面γ,α∩β=l,那么l⊥γ | |
| B. | 如果平面α⊥平面β,那么平面α内一定存在直线平行于平面β | |
| C. | 如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β | |
| D. | 如果平面α⊥平面β,α∩β=l,过α内任意一点作l的垂线m,则m⊥β |
12.“z1与z2互为共轭复数”是“z1z2∈R”的( )条件.
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要条件 | D. | 既不充分也不必要 |
19.设集合M={1,2},N={a2},则“a=1”是“N是M的子集”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
9.已知集合U=R(R是实数集),A={x|-1≤x≤1},B={x|x2-2x<0},则A∪(∁UB)=( )
| A. | [-1,0] | B. | [1,2] | C. | [0,1] | D. | (-∞,1]∪[2,+∞) |
6.变量x,y之间的一组相关数据如表所示:
若x,y之间的线性回归方程为$\widehaty$=$\widehatb$x+12.28,则$\widehatb$的值为( )
| x | 4 | 5 | 6 | 7 |
| y | 8.2 | 7.8 | 6.6 | 5.4 |
| A. | -0.92 | B. | -0.94 | C. | -0.96 | D. | -0.98 |
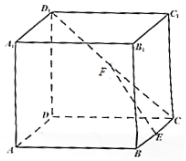 如图,在正方体ABCD-A1B1C1D1中,E、F分别是线段BC、CD1的中点.
如图,在正方体ABCD-A1B1C1D1中,E、F分别是线段BC、CD1的中点.