题目内容
7. 某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)在某一个周期内的图象时,列表并填入的部分数据如表:
某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)在某一个周期内的图象时,列表并填入的部分数据如表:| x | x1 | $\frac{1}{3}$ | x2 | $\frac{7}{3}$ | x3 |
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| Asin(ωx+φ) | 0 | $\sqrt{3}$ | 0 | -$\sqrt{3}$ | 0 |
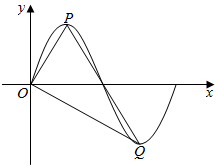
(2)将f(x)的图象沿x轴向右平移$\frac{2}{3}$个单位得到函数g(x)的图象,P、Q分别为函数g(x)图象的最高点和最低点(如图),求∠OQP的大小;
(3)求△OQP的面积.
分析 (1)由函数的最值求出A,由周期求出ω,由五点法作图求出φ的值,可得函数的解析式.
(2)根据y=Asin(ωx+φ)的图象变换规律,求得g(x)的解析式,可得P、Q、M的坐标,利用两个向量的夹角公式求得∠OQP的余弦值,可得∠OQP的值.
(3)根据根据函数图象的对称性可知线段PQ必过点M,由 S△OQP=S△POM+S△QOM,求得它的值.
解答 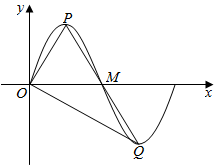 解:(1)由题意可得A=$\sqrt{3}$,$\frac{1}{2}$•$\frac{2π}{ω}$=$\frac{7}{3}$-$\frac{1}{3}$,求得ω=$\frac{π}{2}$.
解:(1)由题意可得A=$\sqrt{3}$,$\frac{1}{2}$•$\frac{2π}{ω}$=$\frac{7}{3}$-$\frac{1}{3}$,求得ω=$\frac{π}{2}$.
再根据五点法作图可得$\frac{π}{2}$•$\frac{1}{3}$+ϕ=$\frac{π}{2}$,∴ϕ=$\frac{π}{3}$,
∴f(x)=$\sqrt{3}$sin($\frac{π}{2}$x+$\frac{π}{3}$).
(2)将f(x)的图象沿x轴向右平移$\frac{2}{3}$个单位得到
函数对应的解析式为 $g(x)=\sqrt{3}sin\frac{π}{2}x$,
因为P、Q分别为该图象的最高点和最低点,
所以,$P(1,\sqrt{3}),Q(3,-\sqrt{3})$,
所以,$\overrightarrow{QO}=(-3,\sqrt{3}),\overrightarrow{QP}=(-2,2\sqrt{3})$,$|\overrightarrow{QO}|=\sqrt{12},|\overrightarrow{QP}|=4,\overrightarrow{QO}•\overrightarrow{QP}=12$,
∴$cos∠OQP=\frac{{\overrightarrow{QO}•\overrightarrow{QP}}}{{|\overrightarrow{QO}||\overrightarrow{QP}|}}=\frac{12}{{2\sqrt{3}×4}}=\frac{{\sqrt{3}}}{2}$,
所以$∠OQP=\frac{π}{6}$.
(3)$OM=\frac{T}{2}=2$,根据函数图象的对称性可知线段PQ必过点M(如图),
∴S△OQP=S△POM+S△QOM=$\frac{1}{2}$|yP|•OM+$\frac{1}{2}$|yQ|•OM=|yP|•OM=2$\sqrt{3}$.
点评 本题主要考查利用y=Asin(ωx+φ)的图象特征,由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的最值求出A,由周期求出ω,由五点法作图求出φ的值;还考查了y=Asin(ωx+φ)的图象变换规律,两个向量的夹角公式,属于中档题.

 名校课堂系列答案
名校课堂系列答案
| A. | 15 | B. | 23 | C. | 47 | D. | 95 |
| A. | (¬p)∨q | B. | p∧q | C. | (¬p)∧(¬q) | D. | (¬p)∨(¬q) |
| A. | -3 | B. | -1 | C. | 1 | D. | 3 |
| A. | 3a2cosa+10ax2 | B. | 3a2cosa+10ax2+10a2x | ||
| C. | a3sina+10a2x | D. | 10a2x |
| A. | $\underbrace{33…3}_{n个}$ | B. | $\underbrace{33…3}_{n+1个}$ | C. | $\underbrace{33…3}_{2n个}$ | D. | $\underbrace{33…3}_{2n-1个}$ |