题目内容
12.已知O是△ABC所在平面内一点,D为BC边中点.(1)若点O满足$2\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow 0$,求证:$\overrightarrow{AO}=\overrightarrow{OD}$;
(2)已知E为AC边中点,O在线段DE上,且满足$\overrightarrow{OA}+2\overrightarrow{OB}+3\overrightarrow{OC}=\overrightarrow 0$,△BOC的面积为2,求△ABC的面积.
分析 (1)根据D为BC的中点,从而根据向量加法的平行四边形法则得到$\overrightarrow{OB}+\overrightarrow{OC}=2\overrightarrow{OD}$,从而得到$2\overrightarrow{OA}+2\overrightarrow{OD}=\overrightarrow{0}$,这便可得出$\overrightarrow{AO}=\overrightarrow{OD}$;
(2)同上$\overrightarrow{OA}+\overrightarrow{OC}=2\overrightarrow{OE}$,从而得到$\overrightarrow{OE}=2\overrightarrow{DO}$,进一步便可得到AB=6DO,从而有S△ABC=6S△BOC,这样便可得出△ABC的面积.
解答 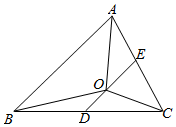 解:(1)∵D为BC边中点;
解:(1)∵D为BC边中点;
∴$\overrightarrow{OB}+\overrightarrow{OC}=2\overrightarrow{OD}$;
∴由$2\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{0}$得,$2\overrightarrow{OA}+2\overrightarrow{OD}=\overrightarrow{0}$;
∴$\overrightarrow{AO}=\overrightarrow{OD}$;
(2)如图,根据条件:$\overrightarrow{OA}+2\overrightarrow{OB}+3\overrightarrow{OC}=(\overrightarrow{OA}+\overrightarrow{OC})$$+2(\overrightarrow{OB}+\overrightarrow{OC})$
=$2\overrightarrow{OE}+4\overrightarrow{OD}$
=$\overrightarrow{0}$;
∴$\overrightarrow{OE}=2\overrightarrow{DO}$;
∴DE=3DO;
又AB=2DE;
∴AB=6DO;
∴S△ABC=6S△BOC=12;
即△ABC的面积为12.
点评 考查向量加法的平行四边形法则,向量的加法和数乘运算,以及向量数乘的几何意义,三角形的面积公式.

 名校课堂系列答案
名校课堂系列答案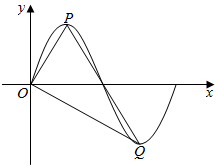 某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)在某一个周期内的图象时,列表并填入的部分数据如表:
某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)在某一个周期内的图象时,列表并填入的部分数据如表:| x | x1 | $\frac{1}{3}$ | x2 | $\frac{7}{3}$ | x3 |
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| Asin(ωx+φ) | 0 | $\sqrt{3}$ | 0 | -$\sqrt{3}$ | 0 |
(2)将f(x)的图象沿x轴向右平移$\frac{2}{3}$个单位得到函数g(x)的图象,P、Q分别为函数g(x)图象的最高点和最低点(如图),求∠OQP的大小;
(3)求△OQP的面积.

| A. | 0 | B. | 3 | C. | 6 | D. | 12 |
| A. | $\frac{2π}{3}$ | B. | $\frac{π}{3}$ | C. | $\frac{3π}{4}$ | D. | $\frac{π}{4}$ |
| A. | $\frac{\sqrt{6}+2}{4}$ | B. | $\frac{\sqrt{6}+\sqrt{2}}{4}$ | C. | $\sqrt{6}$+2 | D. | $\sqrt{6}$+$\sqrt{2}$ |
 某赛季甲,乙两名篮球运动员每场比赛得分情况用茎叶图表示如图:根据以上茎叶图,则甲得分的中位数是26;乙得分的众数是31和36.
某赛季甲,乙两名篮球运动员每场比赛得分情况用茎叶图表示如图:根据以上茎叶图,则甲得分的中位数是26;乙得分的众数是31和36.