题目内容
17．根据$\sqrt{11-2}=3，\sqrt{1111-22}=33，\sqrt{111111-222}=333…$，猜得$\sqrt{\underbrace{11…1}_{2n个1}-\underbrace{22…2}_{n个2}}（{n∈{N^+}}）$的值是（ ）| A． | $\underbrace{33…3}_{n个}$ | B． | $\underbrace{33…3}_{n+1个}$ | C． | $\underbrace{33…3}_{2n个}$ | D． | $\underbrace{33…3}_{2n-1个}$ |
分析 根据已知中的等式，可得3的个数等于根据内2的个数，进而得到答案．
解答 解：∵$\sqrt{11-2}=3，\sqrt{1111-22}=33，\sqrt{111111-222}=333…$，
归纳可得：$\sqrt{\underbrace{11…1}_{2n个1}-\underbrace{22…2}_{n个2}}（{n∈{N^+}}）$=$\underbrace{33…3}_{n个}$，
故选：A
点评 归纳推理的一般步骤是：（1）通过观察个别情况发现某些相同性质；（2）从已知的相同性质中推出一个明确表达的一般性命题（猜想）．
练习册系列答案
补充习题江苏系列答案
学练快车道口算心算速算天天练系列答案
相关题目
7．
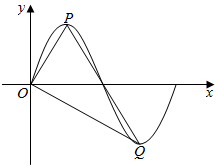某同学用“五点法”画函数f（x）=Asin（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}$）在某一个周期内的图象时，列表并填入的部分数据如表：
（1）请写出上表的x1、x2、x3，并直接写出函数的解析式；
（2）将f（x）的图象沿x轴向右平移$\frac{2}{3}$个单位得到函数g（x）的图象，P、Q分别为函数g（x）图象的最高点和最低点（如图），求∠OQP的大小；
（3）求△OQP的面积．
某同学用“五点法”画函数f（x）=Asin（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}$）在某一个周期内的图象时，列表并填入的部分数据如表：| x | x1 | $\frac{1}{3}$ | x2 | $\frac{7}{3}$ | x3 |
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| Asin（ωx+φ） | 0 | $\sqrt{3}$ | 0 | -$\sqrt{3}$ | 0 |
（2）将f（x）的图象沿x轴向右平移$\frac{2}{3}$个单位得到函数g（x）的图象，P、Q分别为函数g（x）图象的最高点和最低点（如图），求∠OQP的大小；
（3）求△OQP的面积．
2．已知x＞0，y＞0，若不等式a（x+y）≥x+$\sqrt{\frac{1}{2}xy}$恒成立，则a的最小值为（ ）
| A． | $\frac{\sqrt{6}+2}{4}$ | B． | $\frac{\sqrt{6}+\sqrt{2}}{4}$ | C． | $\sqrt{6}$+2 | D． | $\sqrt{6}$+$\sqrt{2}$ |
9．平面几何中，若△ABC的内切圆半径为r，其三边长分别为a，b，c，则△ABC的面积$S=\frac{1}{2}（a+b+c）•r$．类比上述命题，若三棱锥的内切球半径为R，其四个面的面积分别为S1，S2，S3，S4，猜想三棱锥体积V的一个公式．若三棱锥P-ABC的体积V=$\frac{{2\sqrt{2}}}{3}$，其四个面的面积均为$\sqrt{3}$，根据所猜想的公式计算该三棱锥P-ABC的内切球半径R为（ ）
| A． | $\frac{{\sqrt{6}}}{6}$ | B． | $\frac{{\sqrt{6}}}{3}$ | C． | $\frac{{\sqrt{6}}}{12}$ | D． | $\frac{{\sqrt{6}}}{4}$ |
7．设区域Ω={（x，y）|0≤x≤2，0≤y≤2}，区域A={（x，y）|xy≤1，（x，y）∈Ω}，在区域Ω中随机取一个点，则该点在A中的概率（ ）
| A． | $\frac{1+2ln2}{4}$ | B． | $\frac{1+2ln2}{8}$ | C． | $\frac{2ln2}{4}$ | D． | $\frac{1}{2}$ |