题目内容
19．函数f（x）=a3sina+5a2x2的导数f′（x）=（ ）| A． | 3a2cosa+10ax2 | B． | 3a2cosa+10ax2+10a2x | ||
| C． | a3sina+10a2x | D． | 10a2x |
分析 根据函数的导数公式进行求解即可．
解答 解：∵f（x）=a3sina+5a2x2，
∴导数f′（x）=10a2x，
故选：D．
点评 本题主要考查函数的导数的计算，要求熟练掌握掌握常见函数的导数公式，比较基础．
练习册系列答案
通城学典默写能手系列答案
相关题目
9．与双曲线$\frac{{x}^{2}}{2}$-y2=1有相同渐近线，且与椭圆$\frac{y^2}{8}+\frac{x^2}{2}=1$有共同焦点的双曲线方程是（ ）
| A． | $\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{4}$=1 | B． | $\frac{{y}^{2}}{2}$-$\frac{{x}^{2}}{4}$=1 | C． | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{2}$=1 | D． | $\frac{{y}^{2}}{4}$-$\frac{{y}^{2}}{2}$=1 |
10．函数f（x）与g（x）=（$\frac{1}{2}$）x的图象关于直线y=x对称，则f（x2-2x）的单增区间为（ ）
| A． | （-∞，0） | B． | （2，+∞） | C． | （0，1） | D． | [1，2） |
7．
某同学用“五点法”画函数f（x）=Asin（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}$）在某一个周期内的图象时，列表并填入的部分数据如表：
（1）请写出上表的x1、x2、x3，并直接写出函数的解析式；
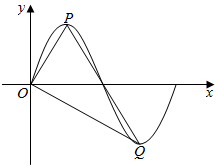
（2）将f（x）的图象沿x轴向右平移$\frac{2}{3}$个单位得到函数g（x）的图象，P、Q分别为函数g（x）图象的最高点和最低点（如图），求∠OQP的大小；
（3）求△OQP的面积．
某同学用“五点法”画函数f（x）=Asin（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}$）在某一个周期内的图象时，列表并填入的部分数据如表：| x | x1 | $\frac{1}{3}$ | x2 | $\frac{7}{3}$ | x3 |
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| Asin（ωx+φ） | 0 | $\sqrt{3}$ | 0 | -$\sqrt{3}$ | 0 |
（2）将f（x）的图象沿x轴向右平移$\frac{2}{3}$个单位得到函数g（x）的图象，P、Q分别为函数g（x）图象的最高点和最低点（如图），求∠OQP的大小；
（3）求△OQP的面积．
14．已知扇形的半径是16，圆心角是2弧度，则扇形的弧长是（ ）
| A． | 64 | B． | 48 | C． | 32 | D． | 16 |
4．根据如图所示程序框图，若输入m=42，n=30，则输出m的值为（ ）
| A． | 0 | B． | 3 | C． | 6 | D． | 12 |
11．把分别标有“诚”“信”“考”“试”的四张卡片随意的排成一排，则能使卡片从左到右可以念成“诚信考试”和“考试诚信”的概率是（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{6}$ | C． | $\frac{1}{8}$ | D． | $\frac{1}{12}$ |
9．平面几何中，若△ABC的内切圆半径为r，其三边长分别为a，b，c，则△ABC的面积$S=\frac{1}{2}（a+b+c）•r$．类比上述命题，若三棱锥的内切球半径为R，其四个面的面积分别为S1，S2，S3，S4，猜想三棱锥体积V的一个公式．若三棱锥P-ABC的体积V=$\frac{{2\sqrt{2}}}{3}$，其四个面的面积均为$\sqrt{3}$，根据所猜想的公式计算该三棱锥P-ABC的内切球半径R为（ ）
| A． | $\frac{{\sqrt{6}}}{6}$ | B． | $\frac{{\sqrt{6}}}{3}$ | C． | $\frac{{\sqrt{6}}}{12}$ | D． | $\frac{{\sqrt{6}}}{4}$ |