题目内容
若方程x3-x+1=0在区间（a，b）（a，b，∈Z，且b-a=1）上有一根，则a+b的值为（ ）
| A、-1 | B、-2 | C、-3 | D、-4 |
考点：二分法求方程的近似解
专题：函数的性质及应用
分析：令f（x）=x3-x+1，由题意可得 f（x）在区间（a，b）上有一零点．再利用函数零点的判定定理求得f（x）在区间（-2，-1）有一零点，可得a和b的值，从而求得a+b的值．
解答：
解：令f（x）=x3-x+1，由题意可得 f（x）在区间（a，b）（a，b，∈Z，且b-a=1）上有一零点．
再根据f（-2）=-5＜0，f（-1）=1＞0，f（-2）f（-1）＜0，
故 f（x）在区间（-2，-1）有一零点，可得a=-2、b=-1，∴a+b=-3，
故选：C．
再根据f（-2）=-5＜0，f（-1）=1＞0，f（-2）f（-1）＜0，
故 f（x）在区间（-2，-1）有一零点，可得a=-2、b=-1，∴a+b=-3，
故选：C．
点评：本题主要考查函数的零点的判定定理的应用，根据函数的解析式求函数的值，判断函数的零点所在的区间的方法，属于基础题．
练习册系列答案
优加精卷系列答案
相关题目
函数y=(
)x2+1(x∈[-1，2])的值域为（ ）
| 1 |
| 2 |
A、[
| ||||
B、(0，
| ||||
C、[
| ||||
D、[
|
函数f（x）=
-6+2x的零点一定位于区间（ ）
| 1 |
| x |
| A、（3，4） |
| B、（2，3） |
| C、（1，2） |
| D、（5，6） |
函数f（x）=x-
的零点所在的大致区间是（ ）
| 2 |
| x |
| A、（-4，-2） |
| B、（-2，-1） |
| C、（2，4） |
| D、（4，+∞） |
函数f（x）=x3+3x2+3x的单调增区间为（ ）
| A、（-∞，+∞） |
| B、（-∞，-1） |
| C、（0，+∞） |
| D、（-1，+∞） |
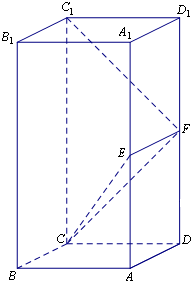在长方体ABCD-A1B1C1D1中，AA1=2AB，E，F分别是AA1，DD1的中点．