题目内容
函数f（x）=x-
的零点所在的大致区间是（ ）
| 2 |
| x |
| A、（-4，-2） |
| B、（-2，-1） |
| C、（2，4） |
| D、（4，+∞） |
考点：二分法求方程的近似解
专题：函数的性质及应用
分析：函数在（-∞，0）上是增函数，求得得f（-2）f（-1）＜0，根据函数的零点的判定定理求得函数f（x）的零点所在的大致区间．
解答：
解：由函数的解析式可得函数在（0，+∞）是增函数，在（-∞，0）上也是增函数．
再根据f（-2）=-1＜，f（-1）=1＞0，可得f（-2）f（-1）＜0，
故函数f（x）=x-
的零点所在的大致区间是（-2，-1），
故选：B．
再根据f（-2）=-1＜，f（-1）=1＞0，可得f（-2）f（-1）＜0，
故函数f（x）=x-
| 2 |
| x |
故选：B．
点评：本题主要考查函数的零点的判定定理的应用，根据函数的解析式求函数的值，判断函数的零点所在的区间的方法，属于基础题．
练习册系列答案
相关题目
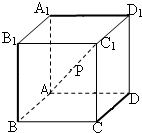在正方体AC1中，若点P在对角线AC1上，且P点到三条棱CD、A1D1、BB1的距离都相等，则这样的点共有（ ）| A、1个 | B、2个 |
| C、3个 | D、无穷多个 |
已知l，m，n是三条不同的直线，α，β是两个不同的平面，下列命题为真命题的是（ ）
| A、若l⊥m，l⊥n，m?α，n?α，则l⊥α |
| B、若l⊥α，α∥β，m?β，则l⊥m |
| C、若l∥m，m?α，则l∥α |
| D、若l⊥α，α⊥β，m?β，则l∥m |
若方程x3-x+1=0在区间（a，b）（a，b，∈Z，且b-a=1）上有一根，则a+b的值为（ ）
| A、-1 | B、-2 | C、-3 | D、-4 |
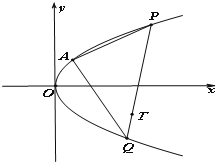如图，已知过点A（1，2）的抛物线C：y2=ax与过点T（3，-2）的动直线l相交于P、Q两点．