题目内容
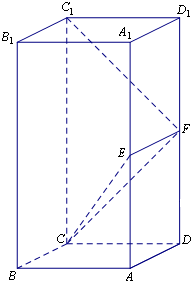 在长方体ABCD-A1B1C1D1中,AA1=2AB,E,F分别是AA1,DD1的中点.
在长方体ABCD-A1B1C1D1中,AA1=2AB,E,F分别是AA1,DD1的中点.(Ⅰ)求证:B1C1∥平面EFC;
(Ⅱ)求证:C1F⊥平面EFC;
(Ⅲ)在棱BB1上是否存在一点P,使得平面ADP⊥平面EFC?若存在,求出
| BP |
| BB1 |
考点:直线与平面垂直的判定,直线与平面平行的判定,平面与平面垂直的性质
专题:空间位置关系与距离
分析:(Ⅰ)由已知条件推导出B1C1∥EF,由此能证明B1C1∥平面EFC.
(Ⅱ)设AB=1,则AA1=2AB=2,D1F=DF=1,所以C1F=CF=
,从而C1F2+CF2=CC12,进而得到C1F⊥CF,由线面垂直得到C1F⊥EF,由此能证明C1F⊥平面EFC.
(Ⅲ)棱BB1上存在中点P,使得平面ADP⊥平面EFC.从而得到平面ADP⊥平面EFC,时
=
.
(Ⅱ)设AB=1,则AA1=2AB=2,D1F=DF=1,所以C1F=CF=
| 2 |
(Ⅲ)棱BB1上存在中点P,使得平面ADP⊥平面EFC.从而得到平面ADP⊥平面EFC,时
| BP |
| BB1 |
| 1 |
| 2 |
解答:
(Ⅰ)证明:∵长方体ABCD-A1B1C1D1中,AA1=2AB,
E,F分别是AA1,DD1的中点,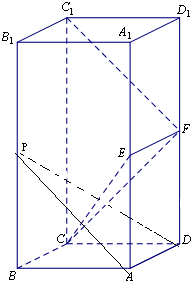
∴B1C1∥A1D1,EF∥A1D1,
∴B1C1∥EF,
∵B1C1不包含于平面EFC,EF?平面EFC,
∴B1C1∥平面EFC.
(Ⅱ)证明:设AB=1,则AA1=2AB=2,D1F=DF=1,
∴C1F=CF=
,∴C1F2+CF2=CC12,
∴C1F⊥CF,∵A1D1⊥平面CDD1C1,EF∥A1D1,
∴EF⊥平面CDD1C1,
∵C1F?平面CDD1C1,∴C1F⊥EF,
∴C1F⊥平面EFC.
(Ⅲ)解:棱BB1上存在中点P,使得平面ADP⊥平面EFC.
证明如下:∵长方体ABCD-A1B1C1D1中,F是DD1中点,P是BB1中点,
∴C1F∥AP,∵C1F⊥平面EFC,∴AP⊥平面EFC,
∵AP?平面ADP,∴平面ADP⊥平面EFC,
此时
=
.
E,F分别是AA1,DD1的中点,

∴B1C1∥A1D1,EF∥A1D1,
∴B1C1∥EF,
∵B1C1不包含于平面EFC,EF?平面EFC,
∴B1C1∥平面EFC.
(Ⅱ)证明:设AB=1,则AA1=2AB=2,D1F=DF=1,
∴C1F=CF=
| 2 |
∴C1F⊥CF,∵A1D1⊥平面CDD1C1,EF∥A1D1,
∴EF⊥平面CDD1C1,
∵C1F?平面CDD1C1,∴C1F⊥EF,
∴C1F⊥平面EFC.
(Ⅲ)解:棱BB1上存在中点P,使得平面ADP⊥平面EFC.
证明如下:∵长方体ABCD-A1B1C1D1中,F是DD1中点,P是BB1中点,
∴C1F∥AP,∵C1F⊥平面EFC,∴AP⊥平面EFC,
∵AP?平面ADP,∴平面ADP⊥平面EFC,
此时
| BP |
| BB1 |
| 1 |
| 2 |
点评:本题考查直线与平面平行的证明,考查直线与平面垂直的证明,考查平面与平面垂直时点的位置的确定,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
若方程x3-x+1=0在区间(a,b)(a,b,∈Z,且b-a=1)上有一根,则a+b的值为( )
| A、-1 | B、-2 | C、-3 | D、-4 |
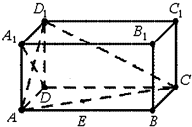 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2. 先阅读如图所示框图,再解答有关问题:
先阅读如图所示框图,再解答有关问题: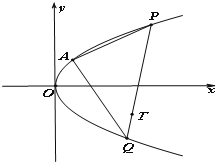 如图,已知过点A(1,2)的抛物线C:y2=ax与过点T(3,-2)的动直线l相交于P、Q两点.
如图,已知过点A(1,2)的抛物线C:y2=ax与过点T(3,-2)的动直线l相交于P、Q两点.