题目内容
写出-720°到720°之间与-1050°终边相同的角的集合 .
考点:终边相同的角
专题:三角函数的求值
分析:与-1050°终边相同的角的集合={x|x=-1050°+k•360°,k∈Z}.取k=1,2,3,4即可得出.
解答:
解:与-1050°终边相同的角的集合={x|x=-1050°+k•360°,k∈Z}.
取k=1时,x=-690°;取k=2时,x=-330°;取k=3时,x=30°;取k=4时,x=390°.
∴-720°到720°之间与-1050°终边相同的角的集合为{-690°,-330°,30°,390°}.
故答案为:{-690°,-330°,30°,390°}.
取k=1时,x=-690°;取k=2时,x=-330°;取k=3时,x=30°;取k=4时,x=390°.
∴-720°到720°之间与-1050°终边相同的角的集合为{-690°,-330°,30°,390°}.
故答案为:{-690°,-330°,30°,390°}.
点评:本题考查了终边相同的角的集合,属于基础题.

练习册系列答案
相关题目
 空间四边形PABC的各边及对角线长度都相等,D、E、F分别是AB、BC、CA的中点,下列四个结论中不成立的是( )
空间四边形PABC的各边及对角线长度都相等,D、E、F分别是AB、BC、CA的中点,下列四个结论中不成立的是( )| A、BC∥平面PDF |
| B、平面PDF⊥平面ABC |
| C、BC⊥平面PAE |
| D、平面PAE⊥平面ABC |
方程lnx+x=3的解所在的区间是( )
| A、(0,1) |
| B、(1,2) |
| C、(2,e) |
| D、(e,+∞) |
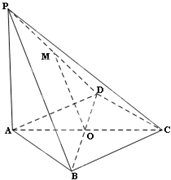 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,点O是对角线AC与BD的交点,M是PD的中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,点O是对角线AC与BD的交点,M是PD的中点.