题目内容
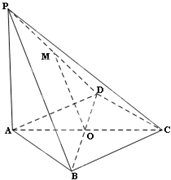 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,点O是对角线AC与BD的交点,M是PD的中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,点O是对角线AC与BD的交点,M是PD的中点.(1)求证:OM∥平面PAB;
(2)平面PBD⊥平面PAC.
考点:平面与平面垂直的判定,直线与平面平行的判定
专题:综合题,空间位置关系与距离
分析:(1)利用三角形中位线的性质,证明线线平行,从而可得线面平行;
(2)先证明BD⊥平面PAC,即可证明平面PBD⊥平面PAC.
(2)先证明BD⊥平面PAC,即可证明平面PBD⊥平面PAC.
解答:
证明:(1)∵在△PBD中,O、M分别是BD、PD的中点,
∴OM是△PBD的中位线,∴OM∥PB,
∵OM?平面PBD,PB?平面PBD,
∴OM∥平面PAB;
(2)∵底面ABCD是菱形,∴BD⊥AC,
∵PA⊥平面ABCD,BD?平面ABCD,∴BD⊥PA.
∵AC?平面PAC,PA?平面PAC,AC∩PA=A,∴BD⊥平面PAC,
∵BD?平面PBD,
∴平面PBD⊥平面PAC.
∴OM是△PBD的中位线,∴OM∥PB,
∵OM?平面PBD,PB?平面PBD,
∴OM∥平面PAB;
(2)∵底面ABCD是菱形,∴BD⊥AC,
∵PA⊥平面ABCD,BD?平面ABCD,∴BD⊥PA.
∵AC?平面PAC,PA?平面PAC,AC∩PA=A,∴BD⊥平面PAC,
∵BD?平面PBD,
∴平面PBD⊥平面PAC.
点评:本小题主要考查空间线面关系等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力.

练习册系列答案
相关题目
 如图,在正方体中,A、B为正方体的两个顶点,M、N、P为所在棱的中点,则异面直线MP、AB在正方体的正视图中的位置关系是( )
如图,在正方体中,A、B为正方体的两个顶点,M、N、P为所在棱的中点,则异面直线MP、AB在正方体的正视图中的位置关系是( )| A、相交 | B、平行 | C、异面 | D、不确定 |
已知点A(-4,0)和B(2,2)M是椭圆
+
=1上一动点,则|MA|+|MB|的最大值( )
| x2 |
| 25 |
| y2 |
| 9 |
A、10+2
| ||
B、
| ||
C、9+
| ||
D、9+2
|
已知x,y∈R+,且(x+1)(y+1)=4,则2x+y的最小值为( )
| A、3 | ||
| B、4 | ||
C、2
| ||
D、4
|
 如图,三棱柱ABC-A1B1C1中,侧棱AA⊥底面ABC,且侧棱和底面边长均为2,D是BC的中点
如图,三棱柱ABC-A1B1C1中,侧棱AA⊥底面ABC,且侧棱和底面边长均为2,D是BC的中点