题目内容
已知函数f（x）=（
sinx+cosx）cosx-
．
（Ⅰ）用五点作图法列表，作出函数f（x）在x∈[0，π]上的图象简图；
（Ⅱ）若f（
+
）=
，-
＜a＜0，求sin（2a-
）的值．
| 3 |
| 1 |
| 2 |
（Ⅰ）用五点作图法列表，作出函数f（x）在x∈[0，π]上的图象简图；
（Ⅱ）若f（
| a |
| 2 |
| π |
| 6 |
| 3 |
| 5 |
| π |
| 2 |
| π |
| 4 |
考点：三角函数中的恒等变换应用,正弦函数的图象
专题：三角函数的求值,三角函数的图像与性质
分析：（Ⅰ）分别取出对应的x值和y值列表，然后描点，再用平滑曲线连接得函数图象．
（Ⅱ）由f（
+
）=
，即可推得cosa=
，从而可求sina的值，进而求出sin2a=2sinacosa=-
，cos2a=2cos2a-1=-
，故可求得sin（2a-
）的值．
（Ⅱ）由f（
| a |
| 2 |
| π |
| 6 |
| 3 |
| 5 |
| 3 |
| 5 |
| 24 |
| 25 |
| 7 |
| 25 |
| π |
| 4 |
解答：
解：（1）f（x）=（
sinx+cosx）cosx-
=
sinxcosx+cos2x-
=
sin2x+
(2cos2x-1)=sin(2x+
)．
列表：
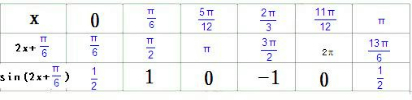
描点画出简图如下：
（2）f（
+
）=sin[2（
+
）+
]=sin（a+
）=cosa=
，
∵-
＜a＜0，∴sina=-
，
∴sin2a=2sinacosa=-
，cos2a=2cos2a-1=-
，
sin（2a-
）=
（sin2a-cos2a）=-
．
| 3 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| π |
| 6 |
列表：
描点画出简图如下：
（2）f（
| a |
| 2 |
| π |
| 6 |
| a |
| 2 |
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
| 3 |
| 5 |
∵-
| π |
| 2 |
| 4 |
| 5 |
∴sin2a=2sinacosa=-
| 24 |
| 25 |
| 7 |
| 25 |
sin（2a-
| π |
| 4 |
| ||
| 2 |
17
| ||
| 50 |
点评：本题主要考察了三角函数中的恒等变换应用，考察了三角函数的图象与性质，属于基础题．
练习册系列答案
相关题目
在直角坐标系中，若α与β的终边互相垂直，那么α与β的关系式为（ ）
| A、β=α+90° |
| B、β=α±90° |
| C、β=α+90°+k•360°（k∈Z） |
| D、β=α±90°+k•360°（k∈Z） |