Question

若P是直角三角形ABC的斜边BC上的一点，且|

AP

|=2，∠BAP=

π

6

，则|

AB

|+

3

|

AC

|的最小值是（　　）

• A、4

  3

• B、4
• C、3+3

  3

• D、3

  3

Answer 1

考点：平面向量数量积的运算

专题：不等式的解法及应用

分析：如图所示，设B（c，0），B（0，b）．由于|

AP

|=2，∠BAP=

π

6

，可得P(

3

，1)．代入直线BC的方程

x

c

+

y

b

=1可得

3

c

+

1

b

=1．因此|

AB

|+

3

|

AC

|=(c+

3

b)(

3

c

+

1

b

)，再利用基本不等式的性质即可得出．

解答： 解：如图所示，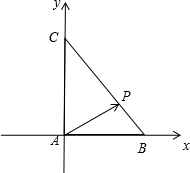
设B（c，0），B（0，b），
∵|

AP

|=2，∠BAP=

π

6

，
∴P(

3

，1)．
直线BC的方程为：

x

c

+

y

b

=1．
∵P是直角三角形ABC的斜边BC上的一点，
∴

3

c

+

1

b

=1．
∴|

AB

|+

3

|

AC

|=(c+

3

b)(

3

c

+

1

b

)
=2

3

+

3b

c

+

c

b

≥2

3

+2

3b c • c b

=4

3

，当且仅当c=

3

b=2

3

时取等号．
∴|

AB

|+

3

|

AC

|的最小值是4

3

．
故选：A．

点评：本题考查了直线的方程、基本不等式的性质，考查了计算能力，属于中档题．